Câu hỏi
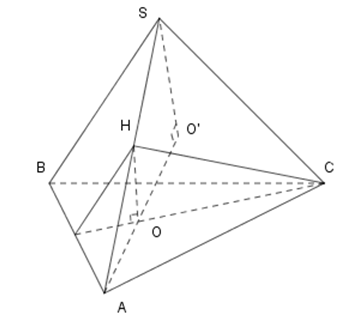
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) đều cạnh \(a,\) tam giác \(SBA\) vuông tại \(B,\) tam giác \(SAC\) vuông tại \(C.\) Biết góc giữa hai mặt phẳng \(\left( SAB \right)\) và \(\left( ABC \right)\) bằng \({{60}^{0}}.\) Tính thể tích khối chóp \(S.ABC\) theo \(a.\)
- A \(\frac{\sqrt{3}{{a}^{3}}}{8}.\)
- B \(\frac{\sqrt{3}{{a}^{3}}}{12}.\)
- C \(\frac{\sqrt{3}{{a}^{3}}}{6}.\)
- D \(\frac{\sqrt{3}{{a}^{3}}}{4}.\)
Phương pháp giải:
Lấy \(K\) là trung điểm của \(AB.\) Lấy \(H\) là trung điểm của \(SA.\) Chứng minh góc giữa \(\left( ABC \right)\) và \(\left( SAB \right)\) bằng \(\widehat{HKC}.\)Từ \(H\) kẻ \(HO\bot CK.\) Kéo dài \(AO\) và hạ \(SO'\bot AO.\) Tính độ dài \(SO'.\) Tính thể tích bằng công thức \({{V}_{S.ABC}}=\frac{1}{3}SO'.{{S}_{SBC}}.\)
Lời giải chi tiết:
Lấy \(K\) là trung điểm của \(AB.\)
Do \(\Delta ABC\) đều nên \(CK\) là đường trung tuyến đồng thời là đường cao \(CK\bot AB.\)
Lấy \(H\) là trung điểm của \(SA.\)
Khi đó \(KH\) là đường trung bình của \(\Delta SAB.\) Kéo theo \(HK//SB.\) Mặt khác \(SB\bot BA\Rightarrow HK\bot BA.\)
Ta có \(\left\{ \begin{align} & CK\bot AB\,\left( CK\in \left( ABC \right) \right) \\ & HK\bot AB\,\left( HK\in \left( SAB \right) \right) \\ \end{align} \right.\) nên góc giữa \(\left( ABC \right)\) và \(\left( SAB \right)\) bằng \(\widehat{HKC}.\)
Từ \(H\) kẻ \(HO\bot CK.\) Ta có \(\left\{ \begin{align} & AB\bot KH \\ & AB\bot KC \\ \end{align} \right.\Rightarrow AB\bot \left( KCH \right)\Rightarrow AB\bot HO.\)
Kết hợp với \(HO\bot CK\) ta suy ra \(HO\bot \left( ABC \right).\)
Khi đó \(SO'//HO.\) Do \(H\) là trung điểm \(AS,SO'//HO\) nên \(HO\) là đường trung bình của \(\Delta SAO'\Rightarrow SO'=\frac{1}{2}HO.\)
\(\Delta SAC\) vuông tại \(C,\,HS=HA\Rightarrow CH\bot SA.\)
Kết hợp với \(CH\bot AB\left( AB\bot \left( KCH \right) \right)\Rightarrow CH\bot \left( SAB \right)\Rightarrow CH\bot KH.\)
Vậy \(\Delta KHC\) vuông tại \(H.\)
Ta chứng minh được \(O\) là trọng tâm của \(\Delta ABC.\)
Do đó \(HO=\tan {{60}^{0}}.\frac{1}{3}KC=\sqrt{3}.\frac{1}{3}.\frac{\sqrt{3}}{2}a=\frac{a}{2}\Rightarrow SO'=a\Rightarrow {{V}_{S.ABC}}=\frac{1}{3}a.\frac{1}{2}.a.\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{12}{{a}^{3}}.\)
Chọn đáp án B.