Câu hỏi
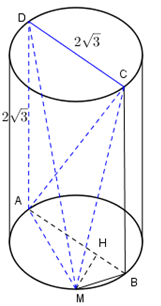
Cho hình trụ có thiết diện qua trục là hình vuông \(ABCD\) cạnh \(2\sqrt{3}\,cm\) với \(AB\) là đường kính của đường tròn đáy tâm \(O.\) Gọi \(M\) là điểm thuộc cung \(\overset\frown{AB}\) của đường tròn đáy sao cho \(\widehat{ABM}={{60}^{0}}.\) Thể tích của khối tứ diện \(ACDM\) là:
- A \(V=3\,\left( c{{m}^{3}} \right).\)
- B \(V=4\,\left( c{{m}^{3}} \right).\)
- C \(V=6\,\left( c{{m}^{3}} \right).\)
- D \(V=7\,\left( c{{m}^{3}} \right).\)
Phương pháp giải:
Xác định đường cao hạ từ \(M\) của tứ diện \(ACDM.\) Tính độ dài đường cao này. Tính diện tích đáy \({{S}_{ACD}}.\) Áp dụng công thức tính thể tích tứ diện để tìm thể tích của \(ACDM.\)
Lời giải chi tiết:
Hạ đường cao \(MH\) xuống \(AB.\)
Khi đó \({{V}_{ACDM}}=\frac{1}{3}MH.{{S}_{ACD}}\,\,\left( 1 \right).\)
\(\Delta ACD\) vuông tại \(D,\) có \(AD=DC=2\sqrt{3}\,\left( cm \right),\) nên \({{S}_{ACD}}=\frac{1}{2}AD.DC=\frac{1}{2}\left( 2\sqrt{3} \right)\left( 2\sqrt{3} \right)=6\,\left( c{{m}^{2}} \right)\,\,\left( 2 \right).\)
Do \(\widehat{ABM}={{60}^{0}}\) và \(\Delta ABM\) vuông tại \(M\) (\(AB\) là đường kính của đáy) nên ta có
\(AM=AB\sin \widehat{ABM}=2\sqrt{3}\sin {{60}^{0}}=3\,\left( cm \right).\)
Áp dụng định lý Py-ta-go cho \(\Delta AMB\) ta có
\(MB=\sqrt{A{{B}^{2}}-A{{M}^{2}}}=\sqrt{{{\left( 2\sqrt{3} \right)}^{2}}-{{3}^{2}}}=\sqrt{3}\,\,\left( cm \right).\)
Áp dụng hệ thức trong tam giác vuông \(ABM\) ta có \(\frac{1}{M{{H}^{2}}}=\frac{1}{A{{M}^{2}}}+\frac{1}{M{{B}^{2}}}=\frac{1}{{{3}^{2}}}+\frac{1}{{{\left( \sqrt{3} \right)}^{2}}}=\frac{4}{9}\Rightarrow MH=\frac{3}{2}\,\left( cm \right)\,\,\left( 3 \right).\)
Thay \(\left( 2 \right),\,\left( 3 \right)\) vào \(\left( 1 \right)\) ta nhận được
\({{V}_{ACDM}}=\frac{1}{3}.\frac{3}{2}.6=3\,\left( c{{m}^{3}} \right).\)
Chọn đáp án A.