Câu hỏi
Một con lắc lò xo dao động điều hoà với tốc độ cực đại bằng 60 cm/s. Chọn gốc toạ độ ở vị trí cân bằng, gốc thời gian lúc vật có động năng bằng thế năng, khi đó vật đang qua li độ x = 3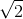
cm theo chiều dương. Phương trình dao động của vật có dạng
- A x = 6cos(10t –π/4) (cm).
- B x = 6
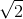cos(10t + π/4) (cm). - C x = 6
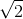cos(10t - π/4) (cm). - D x = 6cos(10t + π/4) (cm).
Phương pháp giải:
Sử dụng lí thuyết về PT dao động \(x = A\cos \left( {\omega t + \varphi } \right)\), trong đó A là biên độ dao động, ω là tốc độ góc, φ là pha dao động tại thời điểm ban đầu; lí thuyết về dao động điều hòa của CLLX
Lời giải chi tiết:
* Tốc độ dao động cực đại của CLLX \({v_{\max }} = \omega A = 60cm/s\)
* Khi vật có động năng bằng thế năng thì li độ của vật là \(x = \pm {A \over {\sqrt 2 }}\)
Vậy PT dao động của CLLX là \(x = 6\cos \left( {10t - {\pi \over 4}} \right)cm\)
=> Chọn đáp án A
Câu hỏi trước
