Câu hỏi
Con lắc đơn gồm quả cầu nhỏ treo vào sợi dây dài 25cm. Kéo vật để dây lệch góc 0,08rad rồi truyền cho vật vận tốc v = 4π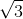 cm/s theo hướng vuông góc với sợi dây và hướng về vị trí cân bằng. Chọn chiều dương là chiều truyền vận tốc, gốc tọa độ ở vị trí cân bằng của vật. Lấy π2 = 10, phương trình li độ góc của vật là
cm/s theo hướng vuông góc với sợi dây và hướng về vị trí cân bằng. Chọn chiều dương là chiều truyền vận tốc, gốc tọa độ ở vị trí cân bằng của vật. Lấy π2 = 10, phương trình li độ góc của vật là
- A \(\alpha = 0,16\cos (2\pi t + {\pi \over 3})rad\)
- B \(\alpha = 0,16\cos (2\pi t - {{2\pi } \over 3})rad\)
- C \(\alpha = 3,47\cos (2\pi t - {{2\pi } \over 3})rad\)
- D \(\alpha = 3,47\cos (2\pi t + {\pi \over 3})rad\)
Phương pháp giải:
Sử dụng lí thuyết về phương trình dao động điều hoà của con lắc đơn
Áp dụng hệ thức độc lập với thời gian của li độ s và vận tốc v để tính biên độ
Sử dụng vòng tròn lượng giác để xác định pha ban đầu.
Lời giải chi tiết:
Ta có : \(\omega = \sqrt {{g \over l}} = 2\sqrt {10} = 2\pi (rad/s) \Rightarrow s = \alpha .l = 2cm\)
Tại thời điểm truyền vận tốc: \( \Rightarrow {s^2} + {\left( {{v \over \omega }} \right)^2} = S_0^2 \Leftrightarrow {S_0} = 4cm \Rightarrow {\alpha _0} = {{{S_0}} \over l} = 0,16rad\)
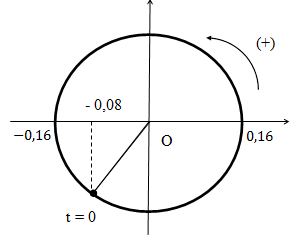
Gốc thời gian là lúc vật qua li độ α = - 0,08 rad theo chiều dương :
=> \(\varphi = - {{2\pi } \over 3}\) rad
Phương trình li độ góc : \(\alpha = {\alpha _0}\cos \left( {\omega t + {\varphi _0}} \right) = 0,16\cos \left( {2\pi t - {{2\pi } \over 3}} \right)rad\)
=> Chọn B