Câu hỏi
Một con lắc đơn chiều dài 20 cm dao động với biên độ góc 60 tại nơi có g = 9,8 m/s2. Chọn gốc thời gian lúc vật đi qua vị trí có li độ góc 30 theo chiều dương thì phương trình li độ góc của vật là
- A α = π/30.sin(7t + 5π/6) rad.
- B α = π/30.sin(7t – 5π/6) rad.
- C α = π/30.sin(7t + π/6) rad.
- D α = π/30.sin(7t – π/6) rad
Phương pháp giải:
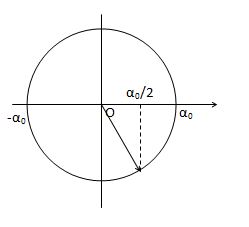
Sử dụng vòng tròn lượng giác, lí thuyết về PT dao động của CLĐ \(\alpha = {\alpha _0}\cos \left( {\omega t + \varphi } \right)\) , trong đó α0 là biên độ dao động, ω là tần độ góc, φ là pha dao động tại thời điểm ban đầu
Lời giải chi tiết:
* Tần số góc của con lắc đơn \(\omega = \sqrt {{g \over l}} = \sqrt {{{9,8} \over {0,20}}} = 7rad/s\)
* Biên độ dao động \({\alpha _0} = {6^0} = {\pi \over {30}}rad\)
* Gốc thời gian là lúc vật đi qua vị trí có li độ góc 30 theo chiều dương => φ = - π/3 rad
Vậy PT dao động α = π/30cos(7t - π/3) rad hay α = π/30.sin(7t + π/6) rad.
=> Chọn đáp án C