Câu hỏi
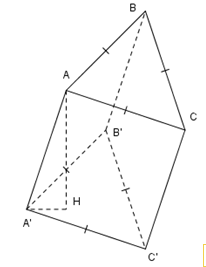
Một khối lăng trụ tam giác có đáy là tam giác đều cạnh \(3,\) cạnh bên bằng \(2\sqrt{3}\) tạo với mặt phẳng đáy một góc\({{30}^{0}}.\). Khi đó thể tích khối lăng trụ là:
- A \(\frac{9}{4}.\)
- B \(\frac{27\sqrt{3}}{4}.\)
- C \(\frac{27}{4}.\)
- D \(\frac{9\sqrt{3}}{4}.\)
Phương pháp giải:
Xác định đường cao của lăng trụ. Sử dụng giả thiết để tìm độ dài đường cao của lăng trụ. Sau đó áp dụng công thức thể tích lăng trụ để tìm thể tích.
Lời giải chi tiết:
Hạ đường cao \(AH\) xuống \(\left( A'B'C' \right).\) Theo giả thiết ta có \(\widehat{AA'H}={{30}^{0}}.\)
Do \(AA'=2\sqrt{3}\) nên ta có
\(sin\widehat{AA'H}=\frac{AH}{AA'}\Rightarrow \sin {{30}^{0}}=\frac{AH}{2\sqrt{3}}\Rightarrow AH=\frac{1}{2}.\left( 2\sqrt{3} \right)=\sqrt{3}.\)
Thể tích của lăng trụ là \(V=AH.{{S}_{A'B'C'}}=\sqrt{3}{{S}_{A'B'C'}}\,\,\left( 1 \right).\)
Do \(A'B'C'\) là tam giác đều có cạnh là \(3\) nên ta có diện tích của tam giác \(A'B'C'\) là \({{S}_{A'B'C'}}=\frac{1}{2}A'B'.B'C'\sin \widehat{A'B'C'}=\frac{1}{2}.3.3.\sin {{60}^{0}}=\frac{9}{2}.\frac{\sqrt{3}}{2}=\frac{9\sqrt{3}}{4}.\)
Thay vào \(\left( 1 \right)\) ta được thể tích \(V=\sqrt{3}.\frac{9\sqrt{3}}{4}=\frac{27}{4}.\)
Chọn đáp án C.