Câu hỏi
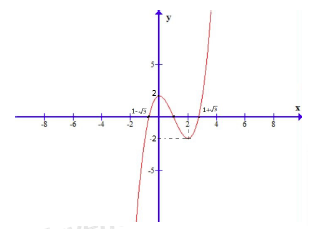
Cho hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 2\) có đồ thị là đường cong trong hình bên. Hỏi phương trình \({\left( {{x^3} - 3{x^2} + 2} \right)^3} - 3{\left( {{x^3} - 3{x^2} + 2} \right)^2} + 2 = 0\) có bao nhiêu nghiệm thực phân biệt?
- A \(7\)
- B \(9\)
- C \(6\)
- D \(5\)
Phương pháp giải:
Phương pháp.Đặt \(t = {x^3} - 3{x^2} + 2.\) Đưa phương trình đã cho về dạng phương trình theo \(t\) tìm nghiệm của phương trình theo \(t\) rồi sử dụng kết quả về đồ thị hàm số để tìm số nghiệm theo \(x\)
Lời giải chi tiết:
Lời giải chi tiết.
Đặt \(t = {x^3} - 3{x^2} + 2.\) Khi đó phương trình đã cho được viết lại thành \({t^3} - 3{t^2} + 2 = 0.\) Ta có
\({t^3} - 3{t^2} + 2 = 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 1 + \sqrt 3 } \right)\left( {t - 1 - \sqrt 3 } \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = 1 - \sqrt 3 \\t = 1 + \sqrt 3 \end{array} \right..\)
Xét phương trình \({x^3} - 3{x^2} + 2 = t.\) Với \(t = 1 \in \left( { - 2,2} \right)\) thì
Đồ thị hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 2\) cắt đường thẳng \(y = a \in \left( { - 2,2} \right)\) tại ba điểm phân biệt, cắt đường thẳng \(y = a,\,\,a = \pm 2\) tại hai điểm phân biệt, và cắt đường thẳng \(y = a,\,\,\left[ \begin{array}{l}a > 2\\a < - 2\end{array} \right.\) tại đúng một điểm. Do đó phương trình \({x^3} - 3{x^2} + 2 = 1 \in \left( { - 2,2} \right)\) có ba nghiệm phân biệt, phương trình ba nghiệm phân biệt, và phương trình \({x^3} - 3{x^2} + 2 = 1 - \sqrt 3 \in \left( { - 2,2} \right)\) chỉ có một nghiệm.
Lưu ý rằng nghiệm của các phương trình \({x^3} - 3{x^2} + 2 = 1,\,\,{x^3} - 3{x^2} + 2 = 1 - \sqrt 3 .{x^3} - 3{x^2} + 2 = 1 + \sqrt 3 \) khác nhau. Do đó số nghiệm của phương trình yêu cầu là: \(3 + 3 + 1 = 7.\)
Chọn đáp án A.







