Phương pháp giải:

\(\frac{f\left( x \right)}{g\left( x \right)}=h\left( x \right)+\frac{c}{g\left( x \right)}\,\,\left( g\left( x \right)\ne 0 \right)\)với c là hằng số.\(\frac{f\left( x \right)}{g\left( x \right)}\in Z\Leftrightarrow \frac{c}{g\left( x \right)}\in Z\Leftrightarrow g\left( x \right)\in U\left( c \right)\)

Lời giải chi tiết:

Gọi điểm \(\left( {{x}_{0}};{{y}_{0}} \right)\,\,\left( {{x}_{0}},{{y}_{0}}\in Z \right)\)là các điểm thuộc đồ thị hàm số cần tìm.Ta có: \({{y}_{0}}=\frac{{{x}_{0}}-1}{{{x}_{0}}+1}=\frac{{{x}_{0}}+1-2}{{{x}_{0}}+1}=1-\frac{2}{{{x}_{0}}+1}\in Z\Leftrightarrow {{x}_{0}}+1\in U\left( 2 \right)=\left\{ \pm 1;\pm 2 \right\}\)

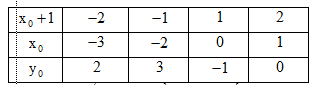
Ta có bảng giá trị sau:

Vậy có 4 điểm thuộc đồ thị hàm số thỏa mãn yêu cầu đề bài.

Chọn C.