Câu hỏi
Cho đồ thị hàm số \((C):y={{x}^{4}}-2{{x}^{2}}.\) Trong các đường thẳng sau dây, đường thẳng nào cắt (C) tại hai điểm phân biệt?
- A \(y=0.\)
- B \(y=1.\)
- C \(y=-\frac{3}{2}.\)
- D \(y=-\frac{1}{2}.\)
Lời giải chi tiết:
Phương pháp:
- Khảo sát hàm số, tìm điều kiện để đường thẳng cứt đồ thị hàm số tại hai điểm phân biệt.
- Kiểm tra các đáp án thỏa điều kiện.
Cách giải:
\(y'=4{{x}^{3}}-4x=0\Leftrightarrow x=0;x=\pm 1\).
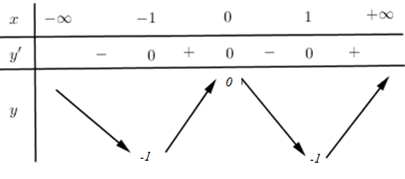
Bảng biến thiên:
Do đó để đường thẳng \(y=m\) cắt \(\left( C \right)\) tại 2 điểm phân biệt thì \(m>0\).
Trong các đáp án chỉ có \(y=1\) thỏa mãn.
Chọn B.
Câu hỏi trước
