Câu hỏi
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
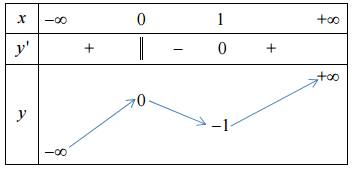
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( {\left| x \right|} \right) = 2m + 1\) có bốn nghiệm phân biệt?
- A \( - \dfrac{1}{2} \leqslant m \leqslant 0\)
- B \( - \dfrac{1}{2} < m < 0\)
- C \( - 1 < m < - \dfrac{1}{2}\)
- D \( - 1 \leqslant m \leqslant - \dfrac{1}{2}\)
Phương pháp giải:
+ Dựng bảng biến thiên của hàm số \(y = f\left( {|x|} \right)\)
Đồ thị hàm số \(y = f\left( {|x|} \right)\) có được bằng cách lấy đối xứng qua trục \(Oy\) phần đồ thị bên phải của hàm số \(y = f\left( x \right)\) và bỏ đi phần đồ thị bên trái trục \(Oy\) của hàm số \(y = f\left( x \right)\).
+ Tìm điều kiện của \(m\) để đường thẳng \(y = 2m + 1\) cắt đồ thị hàm số \(y = f\left( {|x|} \right)\) tại \(4\) điểm phân biệt
Lời giải chi tiết:
Ta có bảng biến thiên của hàm số \(y = f\left( {|x|} \right)\) :

Đường thẳng \(y = 2m + 1\) cắt đồ thị hàm số \(y = f\left( {|x|} \right)\) tại \(4\) điểm phân biệt
\( \Leftrightarrow - 1 < 2m + 1 < 0 \Leftrightarrow - 2 < 2m < - 1 \Leftrightarrow - 1 < m < - \dfrac{1}{2}\)
Chọn đáp án C







