Câu hỏi
Cho khối lăng trụ \(ABC.A'B'C'\)có thể tích bằng \(2018\). Gọi \(M\) là trung điểm \(AA';N, P\) lần lượt là các điểm nằm trên các cạnh \(BB',CC'\) sao cho \(BN = 2B'N,{\text{ }}CP = 3C'P\). Tính thể tích khối đa diện \(ABCMNP\).
- A \(\dfrac{{4036}}{3}\)
- B \(\dfrac{{32288}}{{27}}\)
- C \(\dfrac{{40360}}{{27}}\)
- D \(\dfrac{{23207}}{{18}}\)
Phương pháp giải:
Thể tích \(V\) của khối đa diện \(ABCMNP\) được tính theo công thức \(V = \dfrac{{{V_{ABC.A'B'C'}}}}{3}.\left( {\dfrac{{AM}}{{A'A}} + \dfrac{{BN}}{{B'B}} + \dfrac{{CP}}{{C'C}}} \right)\)
Lời giải chi tiết:
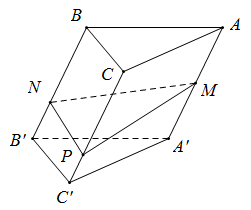
Thể tích cần tìm là \(V = \dfrac{{2018}}{3}\left( {\dfrac{1}{2} + \dfrac{2}{3} + \dfrac{3}{4}} \right) = \dfrac{{23207}}{{18}}\)
Chọn đáp án D
Câu hỏi trước
