Phương pháp giải:

Sử dụng tam giác đồng dạng để tính chiều cao lăng trụ.

Xác định đường vuông góc chung của hai đường thẳng \(AA'\) và \(BC\).

Lời giải chi tiết:

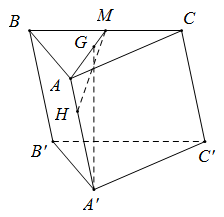
Gọi G là trọng tâm \( \Delta ABC\), \(M\) là trung điểm \(BC\) thì \(A, G, M\) thẳng hàng và \(AM \bot BC,{\text{ }}A'G \bot \left( {ABC} \right) \Rightarrow BC \bot \left( {AA'M} \right)\)

Vẽ \(MH \bot AA'\) tại \(H\) thì \(MH\) là đường vuông góc chung của \(BC\) và \(AA’\)

\(\begin{array}{l}\Delta AGA' \sim \Delta AHM{\rm{ }}\left( {g.g} \right)\\ \Rightarrow \dfrac{{A'G}}{{AG}} = \dfrac{{MH}}{{AH}}\end{array}\)

Có

\(\begin{array}{l}AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\\MH = d\left( {BC;A'A} \right) = \dfrac{{a\sqrt 3 }}{4}\\AH = \sqrt {A{M^2} - M{H^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 3 }}{4}} \right)}^2}} = \dfrac{{3a}}{4}\\ \Rightarrow A'G = \dfrac{{AG.MH}}{{AH}} = \dfrac{a}{3}\end{array}\)

Thể tích lăng trụ \(V = A'G.{S_{ABC}} = \dfrac{a}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)

Chọn đáp án B