Câu hỏi
Cho hình chóp \(S.ABCD \) có đáy \(ABCD\) là hình chữ nhật,\(AB = a,AD = a\sqrt 2 \), đường thẳng \(SA\) vuông góc với mặt phẳng \((ABCD)\); góc giữa đường thẳng \(SC\) và mặt phẳng \((ABCD)\) bằng \({60^0}\). Tính theo \(a\) thể tích khối chóp \(S.ABCD\).
- A \(3\sqrt 2 {a^3}\)
- B \(\sqrt 6 {a^3}\)
- C \(3{a^3}\)
- D \(\sqrt 2 {a^3}\)
Lời giải chi tiết:
Phương pháp: Dựa vào góc giữa \(SC\) và \((ABCD)\) để tính \(SA\) theo \(AC\).
Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(d\) và hình chiếu của nó trên \(\left( P \right)\).
Cách giải
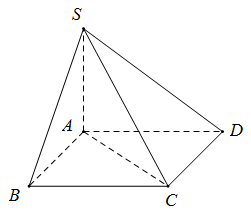
Vì \(SA \bot \left( {ABCD} \right)\) nên góc giữa \(SC\) và \((ABCD)\) là góc \(\widehat {SCA} = {60^0}\)
\(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {A{B^2} + A{D^2}} = a\sqrt 3 \\SA = AC.\tan 60^\circ = a\sqrt 3 .\sqrt 3 = 3a\\{V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABC{\rm{D}}}} = \dfrac{1}{3}SA.AB.AD = {a^3}\sqrt 2 \end{array}\)
Chọn đáp án D
Câu hỏi trước
