Câu hỏi
Cho tích phân \(I = \int\limits_0^{{\pi \over 2}} {\sin x\sqrt {8 + \cos x} dx} \). Đặt \(u = 8 + \cos x\) thì kết quả nào sau đây là đúng?
- A \(I = 2\int\limits_8^9 {\sqrt u du} \)
- B \(I = {1 \over 2}\int\limits_8^9 {\sqrt u du} \)
- C \(I = \int\limits_9^8 {\sqrt u du} \)
- D \(I = \int\limits_8^9 {\sqrt u du} \)
Lời giải chi tiết:
Hướng dẫn giải chi tiết
Đặt \(u = 8 + \cos x \Rightarrow du = - \sin xdx \Rightarrow \sin xdx = - du\)
Đổi cận:
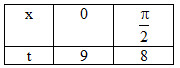
\( \Rightarrow I = - \int\limits_9^8 {\sqrt u du} = \int\limits_8^9 {\sqrt u du} \)
Chọn D.
Câu hỏi trước
