Câu hỏi
Tính tích phân \(I = \int\limits_0^\pi {{{\cos }^3}x\sin xdx} \)
- A \(I = - {1 \over 4}{\pi ^4}\)
- B \(I = - {\pi ^4}\)
- C \(I=0\)
- D \(I = - {1 \over 4}\)
Lời giải chi tiết:
Hướng dẫn giải chi tiết
Đặt \(\cos x = t \Rightarrow - \sin xdx = dt \Rightarrow \sin xdx = - dt\)
Đổi cận
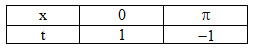
\( \Rightarrow I = - \int\limits_1^{ - 1} {{t^3}dt} = \int\limits_{ - 1}^1 {{t^3}dt} = \left. {{{{t^4}} \over 4}} \right|_{ - 1}^1 = {1 \over 4} - {1 \over 4} = 0\)
Chọn C.







