Lời giải chi tiết:

Hướng dẫn giải chi tiết

Ta có : \({\left( {{a \over b} + {b \over a}} \right)^2} = {{{a^2}} \over {{b^2}}} + 2{a \over b}.{b \over a} + {{{b^2}} \over {{a^2}}} = {{{a^2}} \over {{b^2}}} + {{{b^2}} \over {{a^2}}} + 2 \Rightarrow {{{a^2}} \over {{b^2}}} + {{{b^2}} \over {{a^2}}} = {\left( {{a \over b} + {b \over a}} \right)^2} – 2\)

Biến đổi biểu thức \(P\) về dạng \(P = 3{\left( {{a \over b} + {b \over a}} \right)^2} - 6 - 8\left( {{a \over b} + {b \over a}} \right) = 3{\left( {{a \over b} + {b \over a}} \right)^2} - 8\left( {{a \over b} + {b \over a}} \right) - 6\).

Đặt \(t = {a \over b} + {b \over a} \Rightarrow {t^2} = {\left( {{a \over b} + {b \over a}} \right)^2}\).

Áp dụng bất đẳng thức \({\left( {x + y} \right)^2} \ge 4xy\,\,\forall x,y\) với hai số \({a \over b}\) và \({b \over a}\) ta có : \({t^2} = {\left( {{a \over b} + {b \over a}} \right)^2} \ge 4{a \over b}.{b \over a} = 4 \Leftrightarrow \left| t \right| \ge 2 \Leftrightarrow \left[ \matrix{  t \ge 2 \hfill \cr   t \le  - 2 \hfill \cr}  \right.\)

Biểu thức \(P\) trở thành \(P = 3{t^2} - 8t - 6\).

Trục đối xứng \(x =  - {b \over {2a}} = {4 \over 3}\) và hệ số a = 3 > 0.

Suy ra hàm số \(f\left( t \right) = 3{t^2} - 8t - 6\) nghịch biến trên khoảng \(\left( { - \infty ;\,\,{3 \over 2}} \right)\) và đồng biến trên khoảng\(\left( {{3 \over 2};\,\, + \infty } \right)\).

BBT :

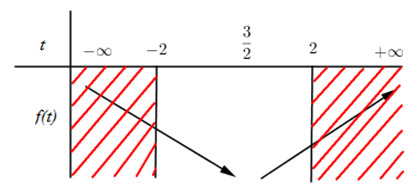
Từ đây suy ra hàm số f(t) đạt giá trị nhỏ nhất tại \(t = {3 \over 2}\)

Ta có \(f\left( {{3 \over 2}} \right) =  - {{45} \over 4}\).

Vậy \(minP = min\,f\left( t \right) =  - {{45} \over 4}\).

Chọn A.