Câu hỏi
Tìm các giá trị của tham số m để phương trình \({1 \over 2}{x^2} - 4\left| x \right| + 3 = {m^2}\) có 3 nghiệm thực phân biệt.
- A \(m = 3\)
- B \( - \sqrt 3 < m < \sqrt 3 \)
- C \(m = \pm \sqrt 3 \)
- D Không tồn tại
Lời giải chi tiết:
Hướng dẫn giải chi tiết
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số \(y = {1 \over 2}{x^2} - 4\left| x \right| + 3 = \left\{ \matrix{ {1 \over 2}{x^2} - 4x + 3\,\,\,\left( {x \ge 0} \right) \hfill \cr {1 \over 2}{x^2} + 4x + 3\,\,\,\,\left( {x < 0} \right) \hfill \cr} \right.\) và đường thẳng \(y = {m^2}\) có tính chất song song với trục hoành.
Đồ thị hàm số \(y = {1 \over 2}{x^2} - 4\left| x \right| + 3\):
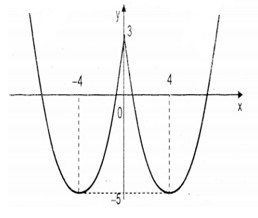
Dựa trên đồ thị ta thấy phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi \({m^2} = 3 \Leftrightarrow m = \pm \sqrt 3 \).
Chọn C.
Câu hỏi trước
