Câu hỏi
Gọi \(S\) là diện tích hình phẳng giới hạn bởi \(f(x) = 12 - 4x\) và \(g(x) = 4\sqrt {9 - {x^2}} \). Biết \(S = a\pi + b(a,b \in \mathbb{R}).\) Tinh \(T = {a^2} + b\).
- A 65 .
- B 64 .
- C 63 .
- D 66 .
Phương pháp giải:
Diện tích giới hạn bởi hai đồ thị: \(\int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
Đặt \(x = a\sin t\) để tính tích phân \(I = \int\limits_a^b {\sqrt {{a^2} - {x^2}} dx} \)
\({\cos ^2}t = \frac{{1 + \cos 2t}}{2}\)
Lời giải chi tiết:
Hoành độ giao điểm của 2 đồ thị là nghiệm của phương trình:
\(12 - 4x = 4\sqrt {9 - {x^2}} \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 0\end{array} \right.\)
\(\begin{array}{l} = > S = \int\limits_0^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \\ = \int\limits_0^3 {\left( {4\sqrt {9 - {x^2}} + 4x - 12} \right)dx} \\ = 4\int\limits_0^3 {\sqrt {9 - {x^2}} dx} + \left. {\left( {2{x^2} - 12x} \right)} \right|_0^3\\ = 4I - 18\end{array}\)
\(I = \int\limits_0^3 {\sqrt {9 - {x^2}} dx} \)
Đặt \(x = \sin t\)
\(dx = \cos tdt\)
Đổi cận:
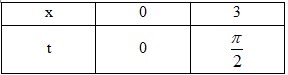
\(\begin{array}{l}I = \int\limits_0^{\frac{\pi }{2}} {3.\left| {\cos t} \right|.3\cos tdt} \\ = \int\limits_0^{\frac{\pi }{2}} {9{{\cos }^2}tdt} \\ = \frac{9}{2}.\left. {\left( {x + \frac{1}{2}\sin 2t} \right)} \right|_0^{\frac{\pi }{2}} = \frac{{9\pi }}{4}\\ \Rightarrow S = 9\pi - 18 \Rightarrow a = 9;b = - 18\\ \Rightarrow T = 63\end{array}\)







