Câu hỏi
Câu 1:
Xét dấu biểu thức \(f\left( x \right) = - {x^2} + 4x + 5\)
Phương pháp giải:
Giải phương trình f(x)=0.
\(a{x^2} + bx + c = 0\) có 2 nghiệm phân biệt \({x_1} < {x_2}\) thì tam thức cùng dấu với a khi \(x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\) và trái dấu với a khi \(x \in \left( {{x_1},{x_2}} \right)\)
Lời giải chi tiết:
\( - {x^2} + 4x + 5 = 0\) có 2 nghiệm phân biệt \(x = - 1;x = 5\).
Khi đó \(f\left( x \right) = - {x^2} + 4x + 5 > 0\) ( trái dấu với -1) khi \(x \in \left( { - 1;5} \right)\) và \(f\left( x \right) = - {x^2} + 4x + 5 < 0\) (cùng dấu với -1) khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {5; + \infty } \right)\)
Câu 2:
Giải bất phương trình \(\left( {x - 1} \right)\left( {{x^2} - 5x + 6} \right) \ge 0\)
Phương pháp giải:
Lập bảng xét dấu.
Lời giải chi tiết:
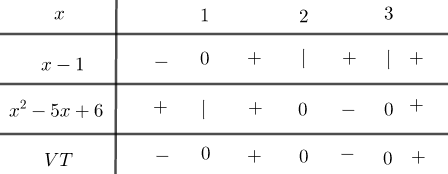
Câu 3:
Giải bất phương trình \(\dfrac{{x + 2}}{{1 - {x^2}}} > 2\)
Phương pháp giải:
Chuyển 2 sang vế trái rồi quy đồng.
Lập bảng xét dấu.
Lời giải chi tiết:
\(\begin{array}{l}\dfrac{{x + 2}}{{1 - {x^2}}} > 2 \Leftrightarrow \dfrac{{x + 2}}{{1 - {x^2}}} - 2 > 0\\ \Leftrightarrow \dfrac{{2{x^2} + x}}{{1 - {x^2}}} > 0 \Leftrightarrow \dfrac{{x\left( {2x + 1} \right)}}{{\left( {1 - x} \right)\left( {1 + x} \right)}} > 0\end{array}\)