Câu hỏi
Cho hình lăng trụ tam giác đều ABC.A’B’C’, gọi G là trọng tâm tam giác ABC. (tham khảo hình vẽ). Khẳng định nào sau đây là sai?
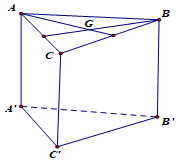
- A \(AG \bot B'C'\).
- B \({\rm{AG}} \bot \left( {BCC'B'} \right)\).
- C \({\rm{AA}}' \bot \left( {ABC} \right)\).
- D \(A'G \bot \left( {ABC} \right)\).
Phương pháp giải:
Lăng trụ tam giác đều là lăng trụ đứng có đáy là tam giác đều.
Lời giải chi tiết:
Do ABC.A’B’C’ là hình lăng trụ tam giác đều nên \(BB' \bot \left( {ABC} \right)\)
\( \Rightarrow BB' \bot AG\left( {AG \subset \left( {ABC} \right)} \right)\)
Do ABC là tam giác đều nên G vừa là trọng tâm vừa là trực tâm. Do đó:
\(\left. \begin{array}{l}AG \bot BC\\AG \bot B{B^\prime }\end{array} \right\} \Rightarrow AG \bot \left( {BC{C^\prime }{B^\prime }} \right)\)
\( \Rightarrow AG \bot {B^\prime }{C^\prime }\)
\(A{A^\prime } \bot (ABC)\) vì \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) là hình lăng trụ đứng.







