Câu hỏi
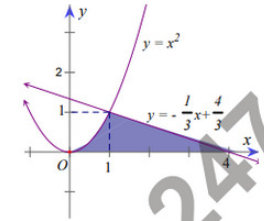
Tính thể tích vật thể tròn xoay ( phần tô đậm) quay quanh trục hoành giới hạn bởi các đường \(y = {x^2}\), \(y = - \frac{1}{3}x + \frac{4}{3}\) và trục hoành như hình vẽ.
- A 1
- B \(\frac{6}{5}\)
- C \(\pi \)
- D \(\frac{{6\pi }}{5}\)
Phương pháp giải:
Tính riêng thể tích \({V_1}\) phần tô đậm từ x=0 đến x=1 và phần thể tích \({V_2}\) từ x=1 đến x=4.
Thể tích cần tìm: \(V = {V_1} + {V_2}\)
Lời giải chi tiết:
Gọi \({V_1}\) là thể tích hình giới hạn bởi đồ thị hàm số \(y = {x^2},y = 0,x = 0,x = 1\).
\({V_2}\) là thể tích hình giới hạn bởi đồ thị hàm số \(y = - \frac{1}{3}x + \frac{4}{3},y = 0,x = 1,x = 4\).
Thể tích cần tìm: \(V = {V_1} + {V_2}\)
Ta có \({V_1} = \pi \int\limits_0^1 {{x^4}dx} = \frac{\pi }{5}\)
\(\begin{array}{l}{V_2} = \pi \int\limits_1^4 {{{\left( { - \frac{1}{3}x + \frac{4}{3}} \right)}^2}dx} = \pi \\ \Rightarrow V = {V_1} + {V_2} = \frac{{6\pi }}{5}\end{array}\)







