Câu hỏi
Trong không gian với hệ trục tọa Oxyz, cho điểm \(M(1;5;2)\) và đường thẳng \(\Delta :\frac{{x + 1}}{2} = \frac{{y - 5}}{1} = \frac{{z + 3}}{1}\). Gọi \((\alpha )\) là mặt phẳng đi qua \(M\) và cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho \(\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\) đạt giá trị nhỏ nhất. Côsin góc giữa đường thẳng \(\Delta \) và đường thẳng BC bằng
- A \(\frac{{\sqrt {147} }}{{58}}\).
- B \(\frac{{\sqrt {174} }}{{85}}\).
- C \(\frac{{\sqrt {417} }}{{58}}\).
- D \(\frac{{\sqrt {174} }}{{58}}\).
Phương pháp giải:
Sử dụng kết quả:
O.ABC có OA, OB, OC đôi một vuông góc với nhau thì hình chiếu của O lên (ABC) là trực tâm của tam giác ABC và \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Tìm điểm H.
Tìm \(\overrightarrow {BC} \).
Góc giữa 2 đường thẳng \(\Delta ,BC\) là: \(\cos \left( {\Delta ,BC} \right) = \frac{{\left| {\overrightarrow {{u_\Delta }} .\overrightarrow {BC} } \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|.\left| {\overrightarrow {BC} } \right|}}\)
Lời giải chi tiết:
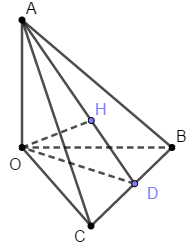
Gọi H là trực tâm tam giác ABC. Vì OA, OB, OC đôi một vuông góc với nhau nên OH là đường cao kẻ từ đỉnh O tới mặt phẳng (ABC).
\(\begin{array}{l} \Rightarrow \frac{1}{{O{H^2}}} = {\left( {\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}} \right)_{\min }}\\ \Leftrightarrow O{H_{\max }}\end{array}\)
Mà \(OH \le OM\) cố định nên \(O{H_{\max }} \Leftrightarrow OH = OM \Leftrightarrow M \equiv H\)
\( \Rightarrow AM \bot BC\)
=> Đường thửng BC nằm trong mặt phẳng (Oyz) và vuông góc với OM.
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {BC} \bot {\overrightarrow n _{\left( {Oyz} \right)}} = \left( {1;0;0} \right)\\\overrightarrow {BC} \bot \overrightarrow {OM} = \left( {1;5;2} \right)\end{array} \right.\)
\(\begin{array}{l} = > \overrightarrow {BC} = \left[ {{{\overrightarrow n }_{\left( {Oyz} \right)}},\overrightarrow {OM} } \right] = \left( {0; - 2;5} \right)\\ = > \cos \left( {\Delta ,BC} \right) = \frac{{\left| {\overrightarrow {{u_\Delta }} .\overrightarrow {BC} } \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{\sqrt {174} }}{{58}}\end{array}\)







