Câu hỏi
Một con lắc đơn gồm vật có khối lượng m, dây treo có chiều dài \(l = 2m\), lấy \(g = {\pi ^2}\left( {m/{s^2}} \right)\). Con lắc dao động điều hòa dưới tác dụng của ngoại lực có biểu thức \(F = {F_0}cos\left( {\omega t + \dfrac{\pi }{2}} \right)\left( N \right)\). Nếu chu kì của ngoại lực tăng từ 4s lên 8s thì biên độ dao động cưỡng bức của vật sẽ
- A luôn tăng
- B giảm rồi tăng.
- C luôn giảm
- D tăng rồi giảm
Phương pháp giải:
+ Vận dụng lí thuyết về dao động cưỡng bức
+ Cộng hưởng dao động
Lời giải chi tiết:
Ta có:
+ Tần số cộng hưởng dao động: \({f_0} = \dfrac{1}{{2\pi }}\sqrt {\dfrac{g}{l}} = \dfrac{1}{{2\sqrt 2 }}\left( {Hz} \right) = 0,354Hz\)
+ Khi chu kì tăng từ 4s lên 8s tương ứng với tần số giảm từ \({f_1} = 0,25Hz\) đến \({f_2} = 0,125Hz\)
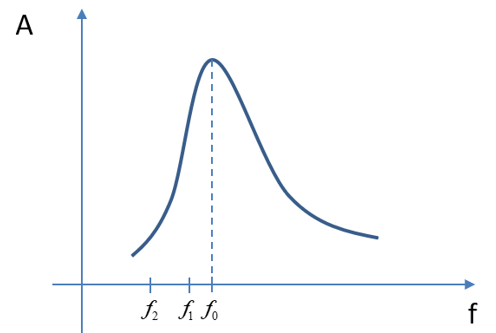
Ta có đồ thị:
Từ đồ thị, ta thấy khi chu kì tăng từ 4s lên 8s thì biên độ dao động cưỡng bức luôn giảm.
Chọn C