Câu hỏi
Cho hàm số\(y = \dfrac{{ax + 1}}{{bx + c}}\) (với a, b, c là các tham số) có bảng biến thiên như sau:
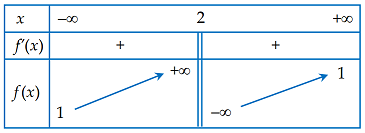
Xét 4 phát biểu sau: (1) \(c > 1\) (2) \(a + b < 0\) (3) \(a + b + c = 0\) (4) \(a > 0\)
Số phát biểu đúng trong 4 phát biểu đã nêu là:
- A \(4\).
- B \(3\).
- C \(2\).
- D \(1\).
Phương pháp giải:
- Dựa vào định nghĩa đường tiệm cận của đồ thị hàm số:
+ Đường thẳng \(y = {y_0}\) là TCN của đồ thị hàm số \(y = f\left( x \right)\) nếu thỏa mãn một trong các điều kiện: \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\), \(\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\).
+ Đường thẳng \(x = {x_0}\) là TCĐ của đồ thị hàm số \(y = f\left( x \right)\) nếu thỏa mãn một trong các điều kiện: \(\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ + } y = - \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = - \infty \).
- Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\,\,\left( {ad \ne bc} \right)\) có TCN \(y = \dfrac{a}{c}\), TCĐ \(x = - \dfrac{d}{c}\).
- Biểu diễn \(a,\,\,c\) theo \(b\), sử dụng giả thiết hàm số đồng biến trên các khoảng xác định giải bất phương trình tìm \(b\). Dựa vào các phát biểu để chọn số phát biểu đúng.
Lời giải chi tiết:
Ta có:
\(\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = 1\) nên \(y = 1\) là đường TCN của đồ thị hàm số ...
\(\,\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = - \infty ,\,\,\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = + \infty \Rightarrow x = - 2\) là TCĐ của đồ thị hàm số \( \Rightarrow \dfrac{{ - c}}{b} = 2 \Leftrightarrow c = - 2b\).
Khi đó ta có \(y = \dfrac{{bx + 1}}{{bx - 2b}}\).
Ta có: \(y' = \dfrac{{ - 2{b^2} - b}}{{{{\left( {bx - 2b} \right)}^2}}}\).
Do hàm số đồng biến trên các khoảng xác định nên \( - 2{b^2} - b > 0 \Leftrightarrow - \dfrac{1}{2} < b < 0\).
\( \Rightarrow \left\{ \begin{array}{l} - \dfrac{1}{2} < a < 0\\ - \dfrac{1}{2} < - 2c < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - \dfrac{1}{2} < a < 0\\0 < c < \dfrac{1}{4}\end{array} \right.\)
Đồng thời \(a + b + c = b + b - 2b = 0\)
Do đó: (1) sai, (2) đúng, (3) đúng, (4) sai.
Vậy có hai phát biểu đúng.
Chọn C.







