Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) cắt trục \(Ox\) tại ba điểm có hoành độ \(a < b < c\) như hình vẽ. Mệnh đề nào dưới đây đúng?
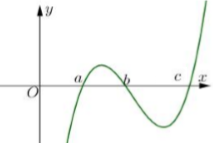
- A \(f\left( b \right) > f\left( a \right) > f\left( c \right)\)
- B \(f\left( a \right) > f\left( b \right) > f\left( c \right)\)
- C \(f\left( b \right) > f\left( c \right) > f\left( a \right)\)
- D \(f\left( c \right) > f\left( b \right) > f\left( a \right)\)
Phương pháp giải:
- Từ đồ thị hàm số \(y = f'\left( x \right)\) lập BBT của hàm số \(f\left( x \right)\).
- Từ BBT so sánh các giá trị \(f\left( a \right),\,\,f\left( b \right),\,\,f\left( c \right)\).
Lời giải chi tiết:
Ta có: \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\\x = b\\x = c\end{array} \right.\).
\(\begin{array}{l}f'\left( x \right) > 0 \Leftrightarrow x \in \left( {a;b} \right) \cup \left( {c; + \infty } \right)\\f'\left( x \right) < 0 \Leftrightarrow x \in \left( { - \infty ;a} \right) \cup \left( {b;c} \right)\end{array}\).
Ta có BBT hàm số \(y = f\left( x \right)\) như sau
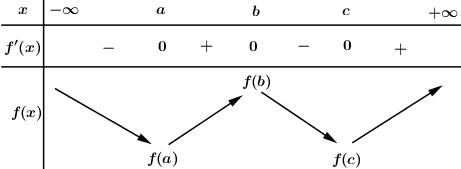
Dựa vào BBT ta thấy trong ba giá trị \(f\left( a \right),\,\,f\left( b \right),\,\,f\left( c \right)\) thì \(f\left( b \right)\) lớn nhất, do đó loại đáp án B, C, D.
Để so sánh \(f\left( a \right),\,\,f\left( c \right)\), ta xét: \(\left\{ \begin{array}{l}{S_1} = \int\limits_a^b {\left| {f'\left( x \right)} \right|dx} = \int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\\{S_2} = \int\limits_b^c {\left| {f'\left( x \right)} \right|dx} = - \int\limits_b^c {f'\left( x \right)dx} = f\left( b \right) - f\left( c \right)\end{array} \right.\).
Dễ dàng nhận thấy \({S_2} > {S_1} \Rightarrow f\left( b \right) - f\left( c \right) > f\left( b \right) - f\left( a \right) \Rightarrow f\left( a \right) > f\left( c \right)\).
Vậy \(f\left( b \right) > f\left( a \right) > f\left( c \right)\).
Chọn A.







