 Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
Câu hỏi
Dao động của một chất điểm có khối lượng \(100\,\,g\) là tổng hợp của hai dao động cùng phương, có phương trình lần lượt là \({x_1} = {A_1}\cos \left( {10\pi t + {\varphi _1}} \right)\) và \({x_2} = {A_2}\cos \left( {10\pi t + {\varphi _2}} \right)\) (\(t\) tính bằng \(s\)). Hình bên là đồ thị biểu diễn mối liên hệ của \({x_1}\) và \({x_2}\). Động năng cực đại của chất điểm là
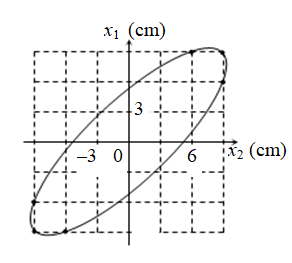
- A \(0,405\,\,J\).
- B \(1,60\,\,J\).
- C \(0,442\,\,J\).
- D \(0,81\,\,J\).
Phương pháp giải:
Sử dụng kĩ năng đọc đồ thị và giản đồ vecto
Biên độ dao động cực đại: \(A=\sqrt{{{A}_{1}}^{2}+{{A}_{2}}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi }\)
Động năng cực đại của chất điểm: \({{\text{W}}_{d\max }}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\)
Lời giải chi tiết:
Từ đồ thị ta lấy 2 điểm với \(\left\{ \begin{align}& {{x}_{1}}=9cm \\& {{x}_{2}}=9cm \\\end{align} \right.\) và \(\left\{ \begin{align}& {{x}_{1}}=9cm \\& {{x}_{2}}=6cm \\\end{align} \right.\), ta có giản đồ vecto:

Trường hợp \({{x}_{1}}={{x}_{2}}=9cm\), ta có: \(x=A\cos \frac{\Delta \varphi }{2}\Rightarrow \Delta \varphi =2\text{ar}\cos \frac{9}{A}\)
Với \(\left\{ \begin{align}& {{x}_{1}}=9cm \\& {{x}_{2}}=6cm \\\end{align} \right.\), ta có: \(\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}=\text{ar}\cos \frac{6}{A}-\text{ar}\cos \frac{9}{A}\)
\(\Rightarrow \Delta \varphi =2\text{ar}\cos \frac{9}{A}=\text{ar}\cos \frac{6}{A}-\text{ar}\cos \frac{9}{A}\)
Sử dụng chức năng SHIFT+SOLVE trong máy tính bỏ túi, ta có:
\(A\approx 9,4\,\,\left( cm \right)\Rightarrow \Delta \varphi =33,{{55}^{0}}\)
Biên độ dao động tổng hợp là:
\({{A}_{0}}=\sqrt{2{{A}^{2}}+2{{A}^{2}}\cos \Delta \varphi }\approx 18\,\,\left( cm \right)\)
Động năng cực đại của vật là:
\({{\text{W}}_{d\max }}=\frac{1}{2}m{{\omega }^{2}}{{A}_{0}}^{2}=\frac{1}{2}.0,1.{{\left( 10\pi \right)}^{2}}.0,{{18}^{2}}=1,62\,\,\left( J \right)\)
Chọn B.






