Câu hỏi
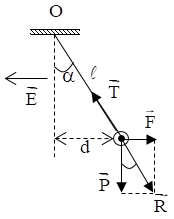
Một quả cầu khối lượng \(m = 4,{5.10^{ - 3}}kg\) treo vào một sợi dây dài \(2m.\) Quả cầu nằm trong điện trường có \(\overrightarrow E \) nằm ngang, hướng sang trái như hình vẽ. Biết \(d = 1m,E = 2000V/m\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Tính điện tích của quả cầu.
- A \(1,{3.10^{ - 5}}C\)
- B \( - 1,{125.10^{ - 5}}C\)
- C \(1,{125.10^{ - 5}}C\)
- D \( - 1,{3.10^{ - 5}}C\)
Phương pháp giải:
Phân tích các lực tác dụng lên quả cầu.
Công thức tính lực điện và trọng lượng: \(\left\{ {\begin{array}{*{20}{l}}{F = qE}\\{P = mg}\end{array}} \right.\)
Sử dụng tỉ số lượng giác trong tam giác vuông suy ra \(E.\)
Lời giải chi tiết:
Lực tác dụng vào quả cầu: \(\overrightarrow P ;\overrightarrow {{F_d}} ;\overrightarrow T \)
Biểu diễn các lực tác dụng vào quả cầu như hình vẽ:
Khi quả cầu cân bằng: \(\overrightarrow P + \overrightarrow {{F_d}} + \overrightarrow T = 0\)
Đặt: \(\overrightarrow R = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow T + \overrightarrow R = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow T \uparrow \downarrow \overrightarrow R \\T = R\,\end{array} \right.\)
Từ hình vẽ ta có:
\(\tan \alpha = \dfrac{d}{{\sqrt {{l^2} - {d^2}} }} = \dfrac{F}{P} \Leftrightarrow \dfrac{1}{{\sqrt {{2^2} - {1^2}} }} = \dfrac{{\left| q \right|E}}{{mg}} \Rightarrow \left| q \right| = \dfrac{{mg}}{{E\sqrt 3 }}\)
\( \Rightarrow \left| q \right| = \dfrac{{4,{{5.10}^{ - 3}}.10}}{{2000\sqrt 3 }} = 1,{3.10^{ - 5}}C\)
Do \(\overrightarrow {{F_d}} \uparrow \downarrow \overrightarrow E \Rightarrow q < 0 \Rightarrow q = - 1,{3.10^{ - 5}}C\)
Chọn D.