20 bài tập Điện trường và cường độ điện trường - đường sức điện mức độ vận dụng cao
Làm đề thiCâu hỏi 1 :
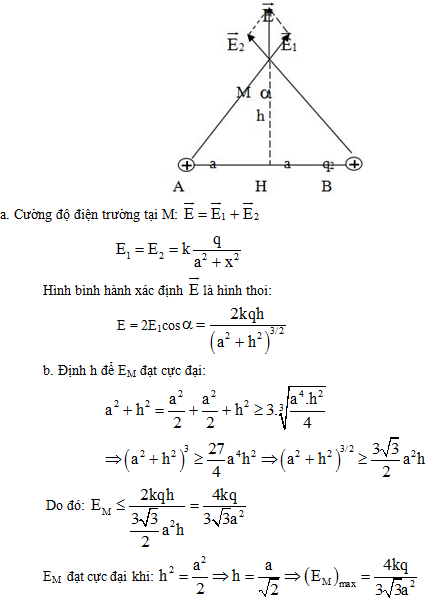
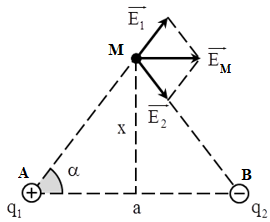
Hai điện tích q1 = q2 = q > 0 đặt tại A và B trong không khí. Cho biết AB = 2a.
a) Xác định cường độ điện trường EM tại điểm M trên đường trung trực của AB, cách AB một đoạn bằng h.
b) Xác định h để EM cực đại. Tính giá trị cực đại này.
Lời giải chi tiết:
Câu hỏi 2 :
Điện tích điểm q1 = 16.10-6 C đặt tại A trong môi trường có hằng điện môi bằng 2.
a) Xác định cường độ điện trường tại điểm B cách A một khoảng 30 cm.
b) Nếu đặt thêm tại B điện tích điểm q2 = 4.10-6 C. Xác định vị trí điểm M tại đó cường độ điện trường bằng không.
Lời giải chi tiết:
Câu hỏi 3 :
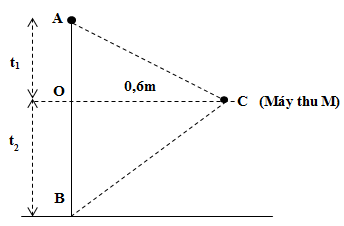
Từ điểm A bắt đầu thả rơi tự do một điện tích điểm ở nơi có gia tốc g = 10m/s2, khi chạm đất tại B nó đứng yên luôn. Tại C cách đoạn thẳng AB 0,6m có một máy đo độ lớn cường độ điện trường. Biết khoảng thời gian từ khi thả điện tích đến khi máy thu M có số chỉ cực đại lớn hơn 0,2s so với khoảng thời gian từ đó đến khi máy thu M có số chỉ không đổi; đồng thời quãng đường sau dài hơn quãng đường trước là 0,2m. Bỏ qua sức cản của không khí và mọi hiệu ứng khác. Tỉ số giữa số đo đầu và số đo cuối của máy đo gần giá trị nào nhất sau đây?
- A 1,85
- B 1,92
- C 1,56
- D 1,35
Đáp án: D
Phương pháp giải:
Cường độ điện trường do điện tích điểm q gây ra: \(E = k{{\left| q \right|} \over {{r^2}}}\)
Quãng đường đi được của vật rơi tự do sau thời gian t: \(s = {{g{t^2}} \over 2} \Rightarrow t = \sqrt {{{2s} \over g}} \)
Lời giải chi tiết:
+ Độ lớn cường độ điện trường đo được ở máy thu M: \(E = k{{\left| q \right|} \over {{r^2}}} \Rightarrow {E_{m{\rm{ax}}}} \Leftrightarrow {r_{\min }} = OC \Rightarrow {E_{m{\rm{ax}}}} = {E_O}\)
+ Công thức tính quãng đường đi được của vật rơi tự do sau thời gian t là: \(s = {{g{t^2}} \over 2} \Rightarrow t = \sqrt {{{2s} \over g}} \)
+ Khoảng thời gian và quãng đường điện tích điểm đi được từ khi thả điện tích đến khi máy thu M có số chỉ cực đại là: \({t_1} = {t_{OA}} = \sqrt {{{2.OA} \over g}} ;{s_1} = OA\)
+ Khoảng thời gian và quãng đường điện tích điểm đi được từ khi máy thu M có số chỉ cực đại đến khi máy thu M có số chỉ không đổi là: \({t_2} = {t_{OB}} = {t_{AB}} - {t_{OA}} = \sqrt {{{2.AB} \over g}} - \sqrt {{{2.OA} \over g}} ;{s_2} = OB\)
+ Theo bài ra ta có:
\(\eqalign{
& \left\{ \matrix{
{t_1} - {t_2} = 0,2s \hfill \cr
{s_2} - {s_1} = OB - OA = 0,2m \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
\sqrt {{{2.OA} \over g}} - \left( {\sqrt {{{2.AB} \over g}} - \sqrt {{{2.OA} \over g}} } \right) = 0,2 \hfill \cr
OB = OA + 0,2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2\sqrt {0,2.OA} - \sqrt {0,2.AB} = 0,2 \hfill \cr
AB = OA + OB = 2.OA + 0,2 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
2\sqrt {0,2.OA} - \sqrt {0,2.\left( {2.OA + 0,2} \right)} = 0,2 \hfill \cr
OB = OA + 0,2 \hfill \cr} \right. \Rightarrow \left\{ \matrix{
OA = \sqrt {0,8} \hfill \cr
OB = \sqrt {0,8} + 0,2 \hfill \cr} \right. \cr} \)
+ Cường độ điện trường tại A và B (số đo đầu và số đo cuối của máy thu):
\(\left\{ \matrix{
{E_A} = k{{\left| q \right|} \over {A{C^2}}} \hfill \cr
{E_B} = k{{\left| q \right|} \over {B{C^2}}} \hfill \cr} \right. \Rightarrow {{{E_A}} \over {{E_B}}} = {{B{C^2}} \over {A{C^2}}} = {{O{B^2} + O{C^2}} \over {O{A^2} + O{C^2}}} = {{{{\left( {\sqrt {0,8} + 0,2} \right)}^2} + {{0,6}^2}} \over {{{\left( {\sqrt {0,8} } \right)}^2} + {{0,6}^2}}} = 1,343\)
Câu hỏi 4 :
Hai điện tích q1 = 5.10-9 C và q2 = - 5.10-9 C đặt tại hai điểm cách nhau 10cm trong chân không. Độ lớn cường độ điện trường tại điểm nằm trên đường thẳng đi qua hai điện tích và cách q1 5cm và cách q2 15 cm là
- A E = 20000V/m.
- B E = 16000V/m.
- C E = 160V/m.
- D E = 200V/m.
Đáp án: B
Phương pháp giải:
Áp dụng nguyên lý chồng chất điện trường. Ta có hình vẽ:
Áp dụng công thức tính cường độ điện trường:
\(E = k.\frac{{\left| Q \right|}}{{{r^2}}}\)
Lời giải chi tiết:
Áp dụng nguyên lý chồng chất điện trường. Ta có hình vẽ:
Vì \(\overrightarrow {{E_1}} \,\, \uparrow \downarrow \,\,\overrightarrow {{E_2}} \Rightarrow E = \left| {{E_1}--{E_2}} \right|\)
Áp dụng công thức tính cường độ điện trường: \(E = k.\frac{{\left| Q \right|}}{{{r^2}}}\)
Ta có :
\(E = \left| {k.\frac{{\left| {{Q_1}} \right|}}{{r_1^2}} - k.\frac{{\left| {{Q_2}} \right|}}{{r_2^2}}} \right| = \left| {{{9.10}^9}.\left( {\frac{{{{5.10}^{ - 9}}}}{{0,05{}^2}}} \right) - {{9.10}^9}.\left( {\frac{{\left| { - {{5.10}^{ - 9}}} \right|}}{{0,{{15}^2}}}} \right)} \right| = \left| {1,{{8.10}^4} - 0,{{2.10}^4}} \right| = 1,{6.10^4}(V/m)\)
Chọn B
Câu hỏi 5 :
Cường độ điện trường do một điện tích điểm sinh ra tại A và B nằm trên cùng một đường sức lần lượt là 25V/m và 49V/m. Cường độ điện trường EM do điện tích nói trên sinh ra tại điểm M (M là trung điểm của đoạn AB) có giá trị bằng:
- A 34V/m.
- B 12V/m.
- C 16,6V/m.
- D 37 V/m
Đáp án: A
Phương pháp giải:
Áp dụng công thức tính cường độ điện trường
\(E = k.\frac{{\left| q \right|}}{{{r^2}}}\)
Vì điểm M là trung điểm của A và B nên
\({r_M} = \frac{{{r_A} + {r_B}}}{2}\)
Lời giải chi tiết:
Áp dụng công thức tính cường độ điện trường ta xác định được cường độ điện trường tại A, B, M như sau :
\(\left\{ \begin{array}{l}
{E_A} = k.\frac{{\left| q \right|}}{{{r_A}^2}} \Rightarrow {r_A} = \sqrt {\frac{{k.\left| q \right|}}{{{E_A}}}} \\
{E_B} = k.\frac{{\left| q \right|}}{{{r_B}^2}} \Rightarrow {r_B} = \sqrt {\frac{{k.\left| q \right|}}{{{E_B}}}} \\
{E_M} = k.\frac{{\left| q \right|}}{{{r_M}^2}}
\end{array} \right.\)
Vì điểm M là trung điểm của A và B nên \({r_M} = \frac{{{r_A} + {r_B}}}{2}\)
Ta có :
\(\begin{array}{l}
{E_M} = k.\frac{{\left| q \right|}}{{{{\left( {\frac{{{r_A} + {r_B}}}{2}} \right)}^2}}} = k.4.\frac{{\left| q \right|}}{{{{\left( {{r_A} + {r_B}} \right)}^2}}}\\
\,\,\,\,\,\,\,\, = 4k.\frac{{\left| q \right|}}{{{{\left( {\sqrt {\frac{{kq}}{{{E_A}}}} + \sqrt {\frac{{kq}}{{{E_B}}}} } \right)}^2}}} = \frac{4}{{{{\left( {\frac{1}{{\sqrt {{E_A}} }} + \frac{1}{{\sqrt {{E_B}} }}} \right)}^2}}}\\
\,\,\,\,\,\,\,\, = \frac{4}{{{{\left( {\frac{1}{{\sqrt {25} }} + \frac{1}{{\sqrt {49} }}} \right)}^2}}} = \frac{{{{4.35}^2}}}{{{{12}^2}}} = 34,02(V/m)
\end{array}\)
Chọn A
Câu hỏi 6 :
Tại 3 đỉnh của tam giác ABC vuông tại A cạnh \(BC = 50cm; AC = 40cm; AB = 30cm\) ta đặt các điện tích \(q_1 = q_2 = q_3 = 10^{ - 9}C.\) Xác định cường độ điện trường tại H với H là chân đường cao kẻ từ A
- A \(400V/m\)
- B \(246V/m\)
- C \(254V/m\)
- D \(175V/m\)
Đáp án: B
Phương pháp giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng hệ thức lượng trong tam giác vuông và áp dụng nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Lời giải chi tiết:
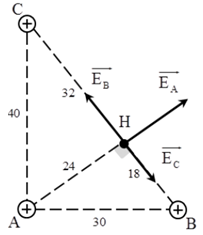
+ Áp dụng hệ thức lượng trong tam giác vuông, ta có: \(HC = 32 cm, HB = 18cm, AH = 24cm.\)
+ Cường độ điện trường do các điện tích gây ra tại H có chiều như hình vẽ
Và có độ lớn lần lượt là:
\(\left\{ \begin{array}{l}{E_A} = k\dfrac{Q}{{A{H^2}}} = {9.10^9}\dfrac{{{{10}^{ - 9}}}}{{0,{{24}^2}}} = 156,25{\mkern 1mu} V/m\\{E_C} = k\dfrac{Q}{{C{H^2}}} = {9.10^9}\dfrac{{{{10}^{ - 9}}}}{{0,{{32}^2}}} = 87,9{\mkern 1mu} V/m\\{E_B} = k\dfrac{Q}{{B{H^2}}} = {9.10^9}\dfrac{{{{10}^{ - 9}}}}{{0,{{18}^2}}} = 277,8{\mkern 1mu} V/m\end{array} \right.\)
+ Cường độ điện trường tổng hợp tại H:
\({E_H} = \sqrt {E_A^2 + {{\left( {{E_B} - {E_C}} \right)}^2}} \approx 246{\mkern 1mu} V/m\)
Chọn B.
Câu hỏi 7 :
Hai điện tích điểm \({q_1} = {2.10^{ - 8}}C;{q_2} = - {3.10^{ - 8}}C\) đặt tại hai điểm A, B trong chân không với \(AB = 30cm.\) Điểm C trong chân không cách A, B lần lượt là \(25cm\) và \(40cm.\) Cho hằng số \(k = 9.10^9\,Nm^2/C^2.\) Cường độ điện trường do hệ hai điện tích gây ra tại C là:
- A \(2568 V/m\)
- B \(4567,5 V/m\)
- C \(4193 V/m\)
- D \(2168,5 V/m\)
Đáp án: D
Phương pháp giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Lời giải chi tiết:
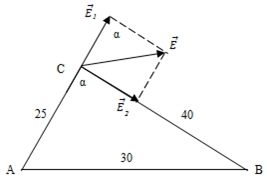
Biểu diễn các vecto cường độ điện trường gây ra tại C trên hình vẽ:
Sử dụng định lí hàm số \(\cos\) trong tam giá ABC có:
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.c{\rm{os}}\alpha \\ \Rightarrow c{\rm{os}}\alpha = \dfrac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}} = \dfrac{{{{25}^2} + {{40}^2} - {{30}^2}}}{{2.25.30}} = 0,6625\end{array}\)
Cường độ điện trường do q1 và q2 lần lượt gây ra tại C:
\(\left\{ \begin{array}{l}{E_1} = \dfrac{{{{9.10}^9}.\left| {{{2.10}^{ - 8}}} \right|}}{{0,{{25}^2}}} = 2880\left( {V/m} \right)\\{E_2} = \dfrac{{{{9.10}^9}.\left| { - {{3.10}^{ - 8}}} \right|}}{{0,{4^2}}} = 1687,5\left( {V/m} \right)\end{array} \right.\)
Cường độ điện trường do hệ hai điện tích gây ra tại C là:
\(E = \sqrt {E_1^2 + E_2^2 - 2{E_1}{E_2}.c{\rm{os}}\alpha } \)
\( \Rightarrow E = \sqrt {{{2880}^2} + 1687,{5^2} - 2.2880.1687,5.0,6625} = 2168,5(V/m)\)
Chọn D.
Câu hỏi 8 :
Hai điện tích \(+ q\) và \( - q\) \((q > 0)\) đặt tại hai điểm A và B với \(AB = 2a.\) M là điểm nằm trên đường trung trực của AB và cách AB một đoạn \(x.\) Xác định \(x\) để cường độ điện trường tại M cực đại, tính giá trị đó.
- A \(x = \dfrac{a}{2};{E_{M\max }} = \dfrac{{k.\left| q \right|}}{{1,25{a^2}}}\)
- B \(x = a;{E_{M\max }} = \dfrac{{k.\left| q \right|}}{{\sqrt 2 {a^2}}}\)
- C \(x = 0;{E_{M\max }} = \dfrac{{2k.\left| q \right|}}{{{a^2}}}\)
- D \(x = 0;{E_{M\max }} = \dfrac{{4k.\left| q \right|}}{{{a^2}}}\)
Đáp án: C
Phương pháp giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Lời giải chi tiết:
Cường độ điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
Ta có: \({E_1} = {E_2} = \dfrac{{k.\left| q \right|}}{{A{M^2}}} = \dfrac{{k.\left| q \right|}}{{{a^2} + {x^2}}}\)
Cường độ điện trường tổng hợp tại M:
\({E_M} = 2{E_1}.cos\alpha = 2.{E_1}.\dfrac{a}{{\sqrt {{a^2} + {x^2}} }} = \dfrac{{2k.\left| q \right|}}{{{a^2} + {x^2}}}.\dfrac{a}{{\sqrt {{a^2} + {x^2}} }} = \dfrac{{2k.\left| q \right|a}}{{{{\left( {{a^2} + {x^2}} \right)}^{1,5}}}}\)
Để \({E_{M\max }} \Rightarrow x = 0 \Rightarrow {E_{M\max }} = \dfrac{{2k.\left| q \right|a}}{{{{\left( {{a^2} + {0^2}} \right)}^{1,5}}}} = \dfrac{{2k.\left| q \right|}}{{{a^2}}}\)
Chọn C.
Câu hỏi 9 :
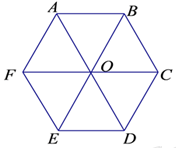
Tại 6 đỉnh của một lục giác đều ABCDEF cạnh \(a = 10cm\) người ta lần lượt đặt các điện tích điểm dương \(q, 2q, 3q, 4q, 5q, 6q.\) Xác định độ lớn cường độ điện trường tại tâm lục giác biết \(q = {10^{ - 7}}C\)?
- A \(5,{4.10^5}V/m\)
- B \({9.10^4}V/m\)
- C \(2,{7.10^5}V/m\)
- D \(18,{9.10^5}V/m\)
Đáp án: A
Phương pháp giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Lời giải chi tiết:
Ta có: \(OA = OB = OC = OD = OE = a\)
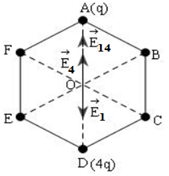
Cường độ điện trường tổng hợp tại O: \(\overrightarrow {{E_O}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} + \overrightarrow {{E_4}} + \overrightarrow {{E_5}} + \overrightarrow {{E_6}} \)
Với: \(\left\{ \begin{array}{l}{E_1} = \dfrac{{kq}}{{{a^2}}};{E_2} = \dfrac{{k2q}}{{{a^2}}} = 2{E_1}\\{E_3} = 3{E_1};{E_4} = 4{E_1};{E_5} = 5{E_1};{E_6} = 6{E_1}\end{array} \right.\)
Có: \(\left\{ \begin{array}{l}\overrightarrow {{E_{14}}} = \overrightarrow {{E_1}} + \overrightarrow {{E_4}} \\\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_4}} \end{array} \right. \Rightarrow {E_{14}} = \left| {{E_1} - {E_4}} \right| = 3{E_1}\)
Tương tự ta có: \(\left\{ \begin{array}{l}\overrightarrow {{E_{25}}} = \overrightarrow {{E_2}} + \overrightarrow {{E_5}} \\\overrightarrow {{E_2}} \uparrow \downarrow \overrightarrow {{E_5}} \end{array} \right. \Rightarrow {E_{25}} = \left| {{E_2} - {E_5}} \right| = 3{E_1}\)
Và: \(\left\{ \begin{array}{l}\overrightarrow {{E_{36}}} = \overrightarrow {{E_3}} + \overrightarrow {{E_6}} \\\overrightarrow {{E_3}} \uparrow \downarrow \overrightarrow {{E_6}} \end{array} \right. \Rightarrow {E_{36}} = \left| {{E_3} - {E_6}} \right| = 3{E_1}\)
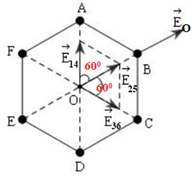
Từ đó ta có hình vẽ :
Từ hình vẽ ta có: \(\overrightarrow {{E_{1436}}} = \overrightarrow {{E_{14}}} + \overrightarrow {{E_{36}}} \)
\( \Rightarrow {E_{1436}} = 2.{E_{14}}.\cos 60 = {E_{14}} = 3{E_1}\)\( \Rightarrow \overrightarrow {{E_O}} = \overrightarrow {{E_{1436}}} + \overrightarrow {{E_{25}}} \)
Với \(\overrightarrow {{E_{1436}}} \uparrow \uparrow \overrightarrow {{E_{25}}} \Rightarrow {E_O} = {E_{1436}} + {E_{25}} = 6{E_1} = 6.\dfrac{{kq}}{{{a^2}}}\)
Thay số ta được:
\({E_O} = 6.\dfrac{{kq}}{{{a^2}}} = \dfrac{{{{6.9.10}^9}{{.10}^{ - 7}}}}{{0,{1^2}}} = 5,{4.10^5}V/m\)
Chọn A.
Câu hỏi 10 :
Cho hình vuông ABCD, tại A và C đặt các điện tích dương \(q_1 = q_3 = q.\) Hỏi phải đặt tại B một điện tích bao nhiêu để cường độ điện trường tại D bằng \(0.\)
- A \(2\sqrt 2 q\)
- B \( - 2\sqrt 2 q\)
- C \(2q\)
- D \( - 2q\)
Đáp án: B
Phương pháp giải:
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lời giải chi tiết:
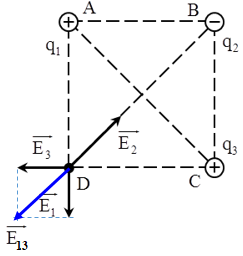
+ Cường độ điện trường tổng hợp tại D:\(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
Trong đó \(\overrightarrow {{E_1}} ;\overrightarrow {{E_2}} ;\overrightarrow {{E_3}} \) lần lượt là vecto cường độ điện trường do các điện tích \({q_1};{q_2};{q_3}\)gây ra tại D.
+ Vì \(\left\{\begin{matrix} q_1 = q_3 \\ AD = CD \end{matrix}\right. \Rightarrow E_1 = E_3 \Rightarrow E_{13} = \sqrt {2}E_1 = \sqrt {2}.\dfrac{k\left | q \right |}{a^2}\)
+ Ta có: \(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} \)
Để cường độ điện trường tại O triệt tiêu thì
\(\overrightarrow {{E_D}} = 0 \Leftrightarrow \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_{13}} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ (1) \( \Rightarrow \overrightarrow {{E_2}} \) hướng lại gần \({q_2} \Rightarrow {q_2} < 0\)
Từ (2) ta có:
\({E_2} = {E_{13}} \Leftrightarrow \dfrac{{k\left| {{q_2}} \right|}}{{{{\left( {a\sqrt 2 } \right)}^2}}} = \sqrt 2 .\dfrac{{k\left| q \right|}}{{{a^2}}} \Rightarrow \left| {{q_2}} \right| = 2\sqrt 2 .\left| q \right| = 2\sqrt 2 \left| q \right|\)
\(\Rightarrow q_2 = - 2\sqrt{2}q.\)
Chọn B.
Câu hỏi 11 :
Tại ba đỉnh A, B và C của một hình vuông ABCD cạnh \(6cm\) trong chân không, đặt ba điện tích điểm \(q_1 = q_3 = 2.10^{ - 7}C\,;\,\,q_2 = - 4.10^{ - 7}C.\) Xác định điện tích \({q_4}\) đặt tại D để cường độ điện trường tổng hợp gây bởi hệ điện tích tại tâm O bằng \(0.\)
- A \( {3.10^{ - 7}}C\)
- B \( - {3.10^{ - 7}}C\)
- C \({4.10^{ - 7}}C\)
- D \( - {4.10^{ - 7}}C\)
Đáp án: D
Phương pháp giải:
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
- Nếu \({q_1};{q_2}\) cùng dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm trong \({q_1};{q_2}\)
- Nếu \({q_1};{q_2}\) trái dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm ngoài \({q_1};{q_2}\)
Lời giải chi tiết:
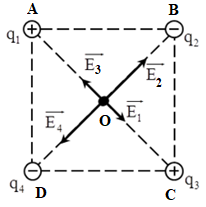
+ Cường độ điện trường tổng hợp tại O:\(\overrightarrow {{E_O}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} + \overrightarrow {{E_4}} \)
Trong đó \(\overrightarrow {{E_1}} ;\overrightarrow {{E_2}} ;\overrightarrow {{E_3}} ;\overrightarrow {{E_4}} \) lần lượt là vecto cường độ điện trường do các điện tích \(q_1\,;\,q_2\,;\,q_3\,;\,q_4\) gây ra tại O.
+ Để cường độ điện trường tại O triệt tiêu thì \(\overrightarrow {{E_O}} = 0\)
+ Vì \(\left\{\begin{matrix} q_1 = q_3 \\ AO = CO \end{matrix}\right. \Rightarrow E_1 = E_3\)
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_3}} \\{E_1} = {E_3}\end{array} \right. \Rightarrow \overrightarrow {{E_{13}}} = \overrightarrow {{E_1}} + \overrightarrow {{E_3}} = 0\)\( \Rightarrow \overrightarrow {{E_O}} = \overrightarrow {{E_2}} + \overrightarrow {{E_4}} \)
Để \(\overrightarrow {{E_O}} = 0 \Leftrightarrow \overrightarrow {{E_2}} + \overrightarrow {{E_4}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_2}} \uparrow \downarrow \overrightarrow {{E_4}} \,\,\left( 1 \right)\\{E_2} = {E_4}\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ (1) \( \Rightarrow \overrightarrow {{E_4}} \) hướng lại gần \({q_4} \Rightarrow {q_4} < 0\)
Từ (2) ta có \({E_4} = {E_2} \Leftrightarrow \dfrac{{k\left| {{q_4}} \right|}}{{O{B^2}}} = \dfrac{{k\left| {{q_2}} \right|}}{{O{B^2}}}\)
\( \Rightarrow \left| {{q_4}} \right| = \left| {{q_2}} \right| = {4.10^{ - 7}}C \Rightarrow {q_4} = - {4.10^{ - 7}}C\)
Chọn D.
Câu hỏi 12 :
Cho hình vuông ABCD, tại A và C đặt các điện tích \(q_1 = q_3 = q = 2,5.10^{ - 8}C.\) Hỏi phải đặt tại B một điện tích bao nhiêu để cường độ điện trường tại D bằng \(0.\)
- A \( - 5\sqrt 2 {.10^{ - 8}}C\)
- B \(5\sqrt 2 {.10^{ - 8}}C\)
- C \({5.10^{ - 8}}C\)
- D \( - {5.10^{ - 8}}C\)
Đáp án: A
Phương pháp giải:
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lời giải chi tiết:
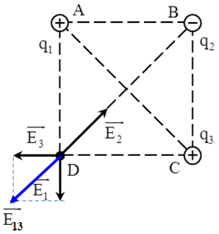
+ Cường độ điện trường tổng hợp tại D:\(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
Trong đó \(\overrightarrow {{E_1}} ;\overrightarrow {{E_2}} ;\overrightarrow {{E_3}} \) lần lượt là vecto cường độ điện trường do các điện tích \({q_1};{q_2};{q_3}\) gây ra tại D.
+ Vì \(\left\{\begin{matrix} q_1 = q_3 \\ AD = CD \end{matrix}\right. \Rightarrow E_1 = E_3 \Rightarrow E_{13} = \sqrt {2}E_1 = \sqrt {2}.\dfrac{k\left | q \right |}{a^2}\)
+ Ta có: \(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} \)
Để cường độ điện trường tại O triệt tiêu thì:
\(\overrightarrow {{E_D}} = 0 \Leftrightarrow \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_{13}} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ (1) \( \Rightarrow \overrightarrow {{E_2}} \) hướng lại gần \({q_2} \Rightarrow {q_2} < 0\)
Từ (2) ta có:
\({E_2} = {E_{13}} \Leftrightarrow \dfrac{{k\left| {{q_2}} \right|}}{{{{\left( {a\sqrt 2 } \right)}^2}}} = \sqrt 2 .\dfrac{{k\left| q \right|}}{{{a^2}}} \Rightarrow \left| {{q_2}} \right| = 2\sqrt 2 .\left| q \right| = 2\sqrt 2 \left| q \right|\)
\(q_2 = - 2\sqrt{2}.2,5.10^{ - 8}C = - 5\sqrt{2}.10^{ - 8}C.\)
Chọn A.
Câu hỏi 13 :
Tại hai đỉnh A, B của một tam giác đều ABC cạnh \(a\) đặt hai điện tích điểm \(q_1 = q_2 = 4.10^{ - 9}C\) trong không khí. Hỏi phải đặt điện tích \({q_3}\) có giá trị bao nhiêu tại C để cường độ điện trường gây ra bởi hệ ba điện tích tại trọng tâm O của tam giác bằng \(0.\)
- A \( - {4.10^{ - 9}}C\)
- B \({4.10^{ - 9}}C\)
- C \({2.10^{ - 9}}C\)
- D \( - {2.10^{ - 9}}C\)
Đáp án: B
Phương pháp giải:
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lời giải chi tiết:
Trọng tâm O của tam giác đều cách đều 3 đỉnh nên: \(OA = OB = OC\)
\( \Rightarrow \left\{ \begin{array}{l}{E_1} = {E_2} = {E_3}\\\left( {\overrightarrow {{E_A}} ;\overrightarrow {{E_B}} } \right) = \left( {\overrightarrow {{E_B}} ;\overrightarrow {{E_C}} } \right) = \left( {\overrightarrow {{E_C}} ;\overrightarrow {{E_A}} } \right) = {120^0}\end{array} \right.\)
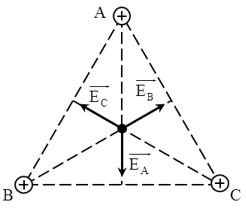
Các điện tích tại các đỉnh A, B, C của tam giác ABC gây ra tại trọng tâm O của tam giác các vecto cường độ điện trường có chiều như hình vẽ:
Với: \(\left\{ \begin{array}{l}{E_A} = {E_B} = \dfrac{{k.\left| {{q_1}} \right|}}{{{{\left( {\dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}} = \dfrac{{2k.{q_1}}}{{{a^2}}}\\{E_C} = \dfrac{{k.\left| {{q_3}} \right|}}{{{{\left( {\dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}} = \dfrac{{3k.{q_3}}}{{{a^2}}}\end{array} \right.\)
Điện trường tổng hợp tại O: \(\overrightarrow {{E_O}} = \overrightarrow {{E_A}} + \overrightarrow {{E_B}} + \overrightarrow {{E_C}} \)
Vì các vecto cường độ điện trường lần lượt hợp nhau một góc \(120^0\) và \(E_A = E_B\) nên:
\(E = 0 \Leftrightarrow q_1 = q_2 = q_3 = 4.10^{ - 9}C\)
Chọn B.
Câu hỏi 14 :
Bốn điểm A, B, C, D trong không khí tạo thành hình chữ nhật ABCD cạnh \(AD = a = 3cm;AB = b = 4cm\). Các điện tích \(q_1\,;\,q_2\,;\,q_3\)được đặt lần lượt tại A, B, C. Biết \(q_2 = - 12,5.10^{ - 8}C\) và cường độ điện trường tổng hợp tại D bằng \(0.\) Tính \({q_1};{q_2}\)?
- A \({q_1} = - 6,{4.10^{ - 8}}C;{q_3} = 2,{7.10^{ - 8}}C\)
- B \({q_1} = 2,{7.10^{ - 8}}C;{q_3} = - 6,{4.10^{ - 8}}C\)
- C \({q_1} = 6,{4.10^{ - 8}}C;{q_3} = 2,{7.10^{ - 8}}C\)
- D \({q_1} = 2,{7.10^{ - 8}}C;{q_3} = 6,{4.10^{ - 8}}C\)
Đáp án: D
Phương pháp giải:
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lời giải chi tiết:
Vectơ cường độ điện trường tại D:
\(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} \)
Do \(\overrightarrow {{E_D}} = 0 \Rightarrow \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_{13}} = {E_2}\end{array} \right.\)
Vì nên \({q_1};{q_3}\) phải là điện tích dương.
Từ hình vẽ ta có:
\(\begin{array}{l}{E_1} = {E_{13}}\cos \alpha = {E_2}.\cos \alpha \Leftrightarrow k.\dfrac{{\left| {{q_1}} \right|}}{{A{D^2}}} = k.\dfrac{{\left| {{q_2}} \right|}}{{B{D^2}}}.\dfrac{{AD}}{{BD}}\\ \Rightarrow \left| {{q_1}} \right| = \dfrac{{A{D^3}}}{{B{D^3}}}.\left| {{q_2}} \right| = \dfrac{{A{D^3}}}{{{{\left( {\sqrt {A{D^2} + A{B^2}} } \right)}^3}}}.\left| {{q_2}} \right|\\ \Rightarrow {q_1} = \dfrac{{{3^3}}}{{{{\left( {\sqrt {{3^2} + {4^2}} } \right)}^3}}}.12,{5.10^{ - 8}} = 2,{7.10^{ - 8}}C\end{array}\)
Tương tự ta có:
\(\begin{array}{l}{E_3} = {E_{13}}\sin \alpha = {E_2}.sin\alpha \Leftrightarrow k.\dfrac{{\left| {{q_3}} \right|}}{{A{B^2}}} = k.\dfrac{{\left| {{q_2}} \right|}}{{B{D^2}}}.\dfrac{{AB}}{{BD}}\\ \Rightarrow \left| {{q_3}} \right| = \dfrac{{A{B^3}}}{{B{D^3}}}.\left| {{q_2}} \right| = \dfrac{{A{B^3}}}{{{{\left( {\sqrt {A{D^2} + A{B^2}} } \right)}^3}}}.\left| {{q_2}} \right|\\ \Rightarrow {q_3} = \dfrac{{{4^3}}}{{{{\left( {\sqrt {{3^2} + {4^2}} } \right)}^3}}}.12,{5.10^{ - 8}} = 6,{4.10^{ - 8}}C\end{array}\)
Chọn D.
Câu hỏi 15 :
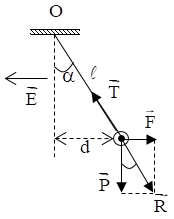
Một quả cầu khối lượng \(m = 4,{5.10^{ - 3}}kg\) treo vào một sợi dây dài \(2m.\) Quả cầu nằm trong điện trường có \(\overrightarrow E \) nằm ngang, hướng sang trái như hình vẽ. Biết \(d = 1m,E = 2000V/m\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Tính điện tích của quả cầu.
- A \(1,{3.10^{ - 5}}C\)
- B \( - 1,{125.10^{ - 5}}C\)
- C \(1,{125.10^{ - 5}}C\)
- D \( - 1,{3.10^{ - 5}}C\)
Đáp án: D
Phương pháp giải:
Phân tích các lực tác dụng lên quả cầu.
Công thức tính lực điện và trọng lượng: \(\left\{ {\begin{array}{*{20}{l}}{F = qE}\\{P = mg}\end{array}} \right.\)
Sử dụng tỉ số lượng giác trong tam giác vuông suy ra \(E.\)
Lời giải chi tiết:
Lực tác dụng vào quả cầu: \(\overrightarrow P ;\overrightarrow {{F_d}} ;\overrightarrow T \)
Biểu diễn các lực tác dụng vào quả cầu như hình vẽ:
Khi quả cầu cân bằng: \(\overrightarrow P + \overrightarrow {{F_d}} + \overrightarrow T = 0\)
Đặt: \(\overrightarrow R = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow T + \overrightarrow R = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow T \uparrow \downarrow \overrightarrow R \\T = R\,\end{array} \right.\)
Từ hình vẽ ta có:
\(\tan \alpha = \dfrac{d}{{\sqrt {{l^2} - {d^2}} }} = \dfrac{F}{P} \Leftrightarrow \dfrac{1}{{\sqrt {{2^2} - {1^2}} }} = \dfrac{{\left| q \right|E}}{{mg}} \Rightarrow \left| q \right| = \dfrac{{mg}}{{E\sqrt 3 }}\)
\( \Rightarrow \left| q \right| = \dfrac{{4,{{5.10}^{ - 3}}.10}}{{2000\sqrt 3 }} = 1,{3.10^{ - 5}}C\)
Do \(\overrightarrow {{F_d}} \uparrow \downarrow \overrightarrow E \Rightarrow q < 0 \Rightarrow q = - 1,{3.10^{ - 5}}C\)
Chọn D.
Câu hỏi 16 :
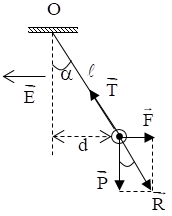
Một quả cầu khối lượng \(m = 4,{5.10^{ - 3}}kg\) treo vào một sợi dây dài \(2m.\) Quả cầu nằm trong điện trường có \(\overrightarrow E \) nằm ngang, hướng sang trái như hình vẽ. Biết \(d = 1m,E = 2000V/m\). Lấy \(g = 10{\rm{ }}m/{s^2}\).
Tính độ lớn của lực căng dây.
- A \(0,09N\)
- B \(0,052N\)
- C \(0,045N\)
- D \(0,156N\)
Đáp án: B
Phương pháp giải:
Phân tích các lực tác dụng lên quả cầu.
Công thức tính lực điện và trọng lượng: \(\left\{ {\begin{array}{*{20}{l}}{F = qE}\\{P = mg}\end{array}} \right.\)
Sử dụng tỉ số lượng giác trong tam giác vuông suy ra \(E.\)
Lời giải chi tiết:
Lực tác dụng vào quả cầu: \(\overrightarrow P ;\overrightarrow {{F_d}} ;\overrightarrow T \)
Biểu diễn các lực tác dụng vào quả cầu như hình vẽ:
Khi quả cầu cân bằng: \(\overrightarrow P + \overrightarrow {{F_d}} + \overrightarrow T = 0\)
Đặt: \(\overrightarrow R = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow T + \overrightarrow R = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow T \uparrow \downarrow \overrightarrow R \\T = R\,\end{array} \right.\)
Từ hình vẽ ta có:
\(\cos \alpha = \dfrac{{\sqrt {{l^2} - {d^2}} }}{l} = \dfrac{P}{R} \Rightarrow R = P.\dfrac{l}{{\sqrt {{l^2} - {d^2}} }} = mg.\dfrac{l}{{\sqrt {{l^2} - {d^2}} }}\)
\( \Rightarrow R = 4,{5.10^{ - 3}}.10.\dfrac{2}{{\sqrt {{2^2} - {1^2}} }} = 0,052N\)
Vậy độ lớn lực căng dây: \(T = R = 0,052N\)
Chọn B.
Câu hỏi 17 :
Một vật hình cầu, có khối lượng riêng của dầu là \({D_1} = 8\left( {kg/{m^3}} \right)\), có bán kính \(R = 1cm,\) tích điện \(q,\) nằm lơ lửng trong không khí trong đó có một điện trường đều. Vectơ cường độ điện trường hướng thẳng đứng từ trên xuống dưới và có độ lớn \(E = 500V/m.\) Khối lượng riêng của không khí là \(D_2 = 1,2\,\,\left ( kg/m^3 \right ).\) Gia tốc trọng trường là \(g = 9,8m/{s^2}\). Chọn phương án đúng.
- A \( - 0,652\mu C\)
- B \( - 0,558\mu C\)
- C \( + 0,652\mu C\)
- D \( + 0,558\mu C\)
Đáp án: B
Phương pháp giải:
Lực điện: \(\overrightarrow {{F_d}} = q.\vec E\)
Nếu: \(\left\{ \begin{array}{l}q > 0 \Rightarrow \overrightarrow {{F_d}} \uparrow \uparrow \overrightarrow E \\q < 0 \Rightarrow \overrightarrow {{F_d}} \uparrow \downarrow \overrightarrow E \end{array} \right.\)
Lời giải chi tiết:
Các lực tác dụng vào giọt dầu: \(\overrightarrow P ;\overrightarrow {{F_A}} ;\overrightarrow {{F_d}} \)
Khi giọt dầu nằm cân bằng thì: \(\overrightarrow P + \overrightarrow {{F_A}} + \overrightarrow {{F_d}} = 0\,\,\left( * \right)\)
Khối lượng và thể tích của giọt dầu:
\(\left\{ \begin{array}{l}P = mg = {D_1}V.g\\V = \dfrac{4}{3}\pi {R^3}\end{array} \right.\)
Lực đẩy Acsimet của không khí tác dụng lên quả cầu:
\({F_A} = {d_{kk}}.V = {D_2}.g.V\)
Vì \({D_1} > {D_2} \Rightarrow P > {F_A} \Rightarrow \overrightarrow {{F_d}} \) hướng lên
\( \Rightarrow \overrightarrow {{F_d}} \uparrow \downarrow \overrightarrow E \Rightarrow q < 0\)
Chiếu (*) lên chiều dương ta được:
\(\begin{array}{l} - P + {F_A} + {F_d} = 0 \Rightarrow - {D_1}.V.g + {D_2}.g.V + \left| q \right|E = 0\\ \Leftrightarrow \left| q \right|E = {D_1}V.g - {D_2}.g.V\\ \Rightarrow \left| q \right| = \dfrac{{V.g\left( {{D_1} + {D_2}} \right)}}{E} = \dfrac{4}{{3E}}\pi {R^3}.g.\left( {{D_1} - {D_2}} \right)\end{array}\)
Do \(q < 0 \Rightarrow q = - \dfrac{4}{{3E}}\pi {R^3}.g.\left( {{D_1} - {D_2}} \right)\)
Thay số ta được:
\(q = - \dfrac{4}{{3.500}}.\pi .0,{01^3}.9,8.\left( {8 - 1,2} \right) = - 5,{558.10^{ - 7}}C\)
Chọn B.
Câu hỏi 18 :
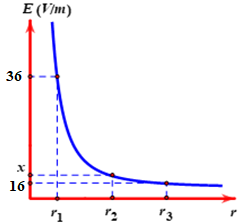
Cường độ điện trường của một điện tích phụ thuộc vào khoảng cách r được mô tả như đồ thị bên. Biết: \(2{{r}_{2}}={{r}_{1}}+{{r}_{3}}\) . Tìm x?
- A 25V/m
- B 30V/m
- C 23,04V/m
- D 28,02V/m
Đáp án: C
Phương pháp giải:
Áp dụng công thức tính cường độ điện trường: \(E=k.\frac{\left| q \right|}{\varepsilon {{r}^{2}}}\)
Vì điểm M là trung điểm của A và B nên: \({{r}_{M}}=\frac{{{r}_{A}}+{{r}_{B}}}{2}\)
Cường độ điện trường tại M: \(\frac{1}{\sqrt{{{E}_{M}}}}=\frac{1}{2}\left( \frac{1}{\sqrt{{{E}_{A}}}}+\frac{1}{\sqrt{{{E}_{B}}}} \right)\)
Lời giải chi tiết:
Ta có: \(2{{r}_{2}}={{r}_{1}}+{{r}_{3}}\Rightarrow {{r}_{2}}=\frac{{{r}_{1}}+{{r}_{3}}}{2}\) \(\Rightarrow {{r}_{2}}\) là trung điểm của \({{r}_{1}}{{r}_{3}}\)
Áp dụng công thức tính cường độ điện trường tại trung điểm ta có:
\(\frac{1}{\sqrt{{{E}_{2}}}}=\frac{1}{2}\left( \frac{1}{\sqrt{{{E}_{1}}}}+\frac{1}{\sqrt{{{E}_{3}}}} \right)\)
Thay số ta được:
\(\frac{1}{\sqrt{x}}=\frac{1}{2}\left( \frac{1}{\sqrt{16}}+\frac{1}{\sqrt{36}} \right)\Rightarrow x=23,04V/m\)
Chọn C.
Tổng hợp 50 bài tập Điện trường và cường độ điện trường - đường sức điện mức độ vận dụng được giải chi tiết giúp các em đạt điểm cao trong các kì thi
Tổng hợp 30 bài tập Điện trường và cường độ điện trường - đường sức điện mức độ, nhận biết, thông hiểu được giải chi tiết giúp các em đạt điểm cao trong các kì thi
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- 40 bài tập Dòng điện trong chân không mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất khí mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất điện phân mức độ vận dụng
- 40 bài tập Dòng điện trong chất điện phân mức độ nhận biết, thông hiểu
- 40 bài tập dòng điện trong kim loại mức độ vận dụng
- 50 bài tập Định luật Ôm đối với toàn mạch mức độ vận dụng (Phần 2)
- 40 bài tập Dòng điện trong chân không mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất khí mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất điện phân mức độ vận dụng
- 40 bài tập Dòng điện trong chất điện phân mức độ nhận biết, thông hiểu