Phương pháp giải:

Công thức tính cường độ điện trường: $E = \dfrac{{k\left| q \right|}}{{{r^2}}}$

Lời giải chi tiết:

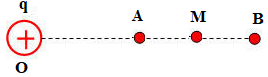
Biểu diễn các điểm trên hình vẽ:

Ta có: $\left\{ \begin{array}{l}{E_A} = \dfrac{{k\left| q \right|}}{{O{A^2}}} = 49V/m\\{E_B} = \dfrac{{k\left| q \right|}}{{O{B^2}}} = 25V/m\\{E_M} = \dfrac{{k\left| q \right|}}{{O{M^2}}}\end{array} \right.$

M là trung điểm của AB nên: $OM = \dfrac{{OA + OB}}{2}$

Lấy $\dfrac{{{E_A}}}{{{E_B}}} = \dfrac{{O{B^2}}}{{O{A^2}}} = \dfrac{{49}}{{25}} \Rightarrow OB = 1,4.OA \Rightarrow OM = 1,2.OA$

Lấy $\dfrac{{{E_A}}}{{{E_M}}} = \dfrac{{O{M^2}}}{{O{A^2}}} = 1,{2^2} \Rightarrow {E_M} = \dfrac{{{E_A}}}{{1,{2^2}}} = \dfrac{{49}}{{1,{2^2}}} = 34,03V/m$

Chọn A.