Câu hỏi
Một con lắc lò xo treo thẳng đứng dao động điều hòa theo phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc lực đàn hồi của lò xo Fđh vào chiều dài l của lò xo.
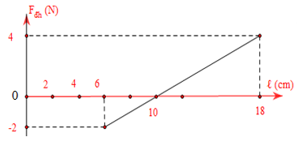
Độ dãn của lò xo tại vị trí cân bằng là
- A 4cm
- B 6cm
- C 8cm
- D 2cm
Phương pháp giải:
Lực đàn hồi = (độ cứng).(độ biến dạng)
Chiều dài cực đại và cực tiểu của lò xo:
\(\left\{ \begin{array}{l}
{l_{m{\rm{ax}}}} = {l_{cb}} + A\\
{l_{\min }} = {l_{cb}} - A
\end{array} \right.\)
Lời giải chi tiết:
Fđh biến thiên từ - 2N đến 4N \(\Rightarrow \) trong quá trình dao động lò xo có thể bị nén, bị dãn và có chiều dài tự nhiên.
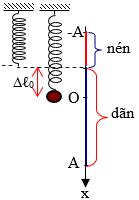
Khi lò xo bị nén cực đại, \({{F}_{dhn}}=k\left( A-\Delta {{l}_{0}} \right)=2N\); lò xo có chiều dài \({{l}_{min}}=6cm\)
Khi \({{F}_{dh}}=0\)lò xo có chiều dài tự nhiên \({{l}_{0}}=10cm\)
Khi lò xo bị dãn cực đại, \({{F}_{dhd}}=k\left( A+\Delta {{l}_{0}} \right)=4\); lò xo có chiều dài \({{l}_{\max }}=18cm\)
\( \Rightarrow \left\{ \begin{array}{l}
{l_{m{\rm{ax}}}} = {l_{cb}} + A\\
{l_{\min }} = {l_{cb}} - A
\end{array} \right. \Rightarrow A = \frac{{{l_{m{\rm{ax}}}} - {l_{min}}}}{2} = \frac{{18 - 6}}{2} = 6cm\)
\(\Rightarrow \frac{{{F}_{dhd}}}{{{F}_{dhn}}}=\frac{A+\Delta {{l}_{0}}}{A-\Delta {{l}_{0}}}=\frac{4}{2}=2\Leftrightarrow \frac{6+\Delta {{l}_{0}}}{6-\Delta {{l}_{0}}}=2\Rightarrow \Delta {{l}_{0}}=2cm\)
Chọn D.







