Câu hỏi
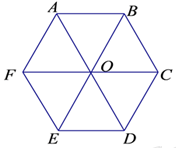
Tại 6 đỉnh của một lục giác đều ABCDEF cạnh \(a = 10cm\) người ta lần lượt đặt các điện tích điểm dương \(q, 2q, 3q, 4q, 5q, 6q.\) Xác định độ lớn cường độ điện trường tại tâm lục giác biết \(q = {10^{ - 7}}C\)?
- A \(5,{4.10^5}V/m\)
- B \({9.10^4}V/m\)
- C \(2,{7.10^5}V/m\)
- D \(18,{9.10^5}V/m\)
Phương pháp giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Lời giải chi tiết:
Ta có: \(OA = OB = OC = OD = OE = a\)
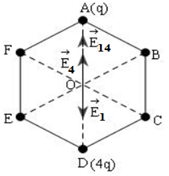
Cường độ điện trường tổng hợp tại O: \(\overrightarrow {{E_O}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} + \overrightarrow {{E_4}} + \overrightarrow {{E_5}} + \overrightarrow {{E_6}} \)
Với: \(\left\{ \begin{array}{l}{E_1} = \dfrac{{kq}}{{{a^2}}};{E_2} = \dfrac{{k2q}}{{{a^2}}} = 2{E_1}\\{E_3} = 3{E_1};{E_4} = 4{E_1};{E_5} = 5{E_1};{E_6} = 6{E_1}\end{array} \right.\)
Có: \(\left\{ \begin{array}{l}\overrightarrow {{E_{14}}} = \overrightarrow {{E_1}} + \overrightarrow {{E_4}} \\\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_4}} \end{array} \right. \Rightarrow {E_{14}} = \left| {{E_1} - {E_4}} \right| = 3{E_1}\)
Tương tự ta có: \(\left\{ \begin{array}{l}\overrightarrow {{E_{25}}} = \overrightarrow {{E_2}} + \overrightarrow {{E_5}} \\\overrightarrow {{E_2}} \uparrow \downarrow \overrightarrow {{E_5}} \end{array} \right. \Rightarrow {E_{25}} = \left| {{E_2} - {E_5}} \right| = 3{E_1}\)
Và: \(\left\{ \begin{array}{l}\overrightarrow {{E_{36}}} = \overrightarrow {{E_3}} + \overrightarrow {{E_6}} \\\overrightarrow {{E_3}} \uparrow \downarrow \overrightarrow {{E_6}} \end{array} \right. \Rightarrow {E_{36}} = \left| {{E_3} - {E_6}} \right| = 3{E_1}\)
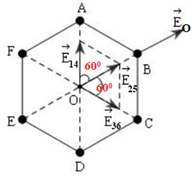
Từ đó ta có hình vẽ :
Từ hình vẽ ta có: \(\overrightarrow {{E_{1436}}} = \overrightarrow {{E_{14}}} + \overrightarrow {{E_{36}}} \)
\( \Rightarrow {E_{1436}} = 2.{E_{14}}.\cos 60 = {E_{14}} = 3{E_1}\)\( \Rightarrow \overrightarrow {{E_O}} = \overrightarrow {{E_{1436}}} + \overrightarrow {{E_{25}}} \)
Với \(\overrightarrow {{E_{1436}}} \uparrow \uparrow \overrightarrow {{E_{25}}} \Rightarrow {E_O} = {E_{1436}} + {E_{25}} = 6{E_1} = 6.\dfrac{{kq}}{{{a^2}}}\)
Thay số ta được:
\({E_O} = 6.\dfrac{{kq}}{{{a^2}}} = \dfrac{{{{6.9.10}^9}{{.10}^{ - 7}}}}{{0,{1^2}}} = 5,{4.10^5}V/m\)
Chọn A.