Câu hỏi
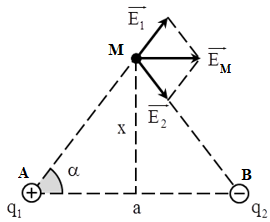
Hai điện tích \(+ q\) và \( - q\) \((q > 0)\) đặt tại hai điểm A và B với \(AB = 2a.\) M là điểm nằm trên đường trung trực của AB và cách AB một đoạn \(x.\) Xác định \(x\) để cường độ điện trường tại M cực đại, tính giá trị đó.
- A \(x = \dfrac{a}{2};{E_{M\max }} = \dfrac{{k.\left| q \right|}}{{1,25{a^2}}}\)
- B \(x = a;{E_{M\max }} = \dfrac{{k.\left| q \right|}}{{\sqrt 2 {a^2}}}\)
- C \(x = 0;{E_{M\max }} = \dfrac{{2k.\left| q \right|}}{{{a^2}}}\)
- D \(x = 0;{E_{M\max }} = \dfrac{{4k.\left| q \right|}}{{{a^2}}}\)
Phương pháp giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Lời giải chi tiết:
Cường độ điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
Ta có: \({E_1} = {E_2} = \dfrac{{k.\left| q \right|}}{{A{M^2}}} = \dfrac{{k.\left| q \right|}}{{{a^2} + {x^2}}}\)
Cường độ điện trường tổng hợp tại M:
\({E_M} = 2{E_1}.cos\alpha = 2.{E_1}.\dfrac{a}{{\sqrt {{a^2} + {x^2}} }} = \dfrac{{2k.\left| q \right|}}{{{a^2} + {x^2}}}.\dfrac{a}{{\sqrt {{a^2} + {x^2}} }} = \dfrac{{2k.\left| q \right|a}}{{{{\left( {{a^2} + {x^2}} \right)}^{1,5}}}}\)
Để \({E_{M\max }} \Rightarrow x = 0 \Rightarrow {E_{M\max }} = \dfrac{{2k.\left| q \right|a}}{{{{\left( {{a^2} + {0^2}} \right)}^{1,5}}}} = \dfrac{{2k.\left| q \right|}}{{{a^2}}}\)
Chọn C.