Câu hỏi
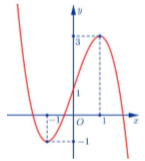
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {f\left( {\cos x} \right)} \right) = m\) có nghiệm thuộc khoảng \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\)?
- A \(2\)
- B \(4\)
- C \(5\)
- D \(3\)
Phương pháp giải:
- Tìm khoảng giá trị của \(\cos x\) với \(x \in \left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\) , từ đó suy ra khoảng giá trị của \(f\left( {\cos x} \right),\,\,f\left( {f\left( {\cos x} \right)} \right)\).
- Phương trình \(f\left( {f\left( {\cos x} \right)} \right) = m\) có nghiệm khi và chỉ khi \(m\) thuộc khoảng giá trị của \(f\left( {f\left( {\cos x} \right)} \right)\).
Câu hỏi trước
