Câu hỏi
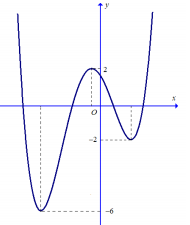
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số thực \(m\) để hàm số \(g\left( x \right) = \left| {f\left( {x + 2020} \right) + {m^2}} \right|\) có 5 điểm cực trị?
- A \(1\)
- B \(2\)
- C \(4\)
- D \(5\)
Lời giải chi tiết:
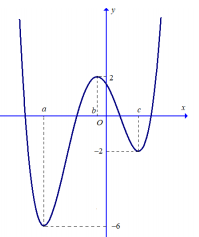
Gọi \(a,\,\,b,\,\,c\,\,\left( {a < b < c} \right)\) là ba điểm cực trị của hàm số \(y = f\left( x \right)\) (như hình vẽ).
Khi đó ta có:
\(\begin{array}{l}f\left( a \right) = - 6\\f\left( b \right) = - 2\\f\left( c \right) = 2\end{array}\)
Xét hàm số \(h\left( x \right) = f\left( {x + 2020} \right)\,\,\,\left( {x \in \mathbb{R}} \right)\) ta có \(h'\left( x \right) = f'\left( {x + 2020} \right)\).
\( \Rightarrow h'\left( x \right) = 0 \Leftrightarrow f'\left( {x + 2020} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x + 2020 = a\\x + 2020 = b\\x + 2020 = c\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = a - 2020\\x = b - 2020\\x = c - 2020\end{array} \right.\).
Ta có BBT hàm số \(h\left( x \right)\) như sau:

Hàm số \(g\left( x \right) = \left| {f\left( {x + 2020} \right) + {m^2}} \right|\) có 5 điểm cực trị khi và chỉ khi \(f\left( {x + 2020} \right) + {m^2} = 0\) có đúng 2 nghiệm không thuộc \(\left\{ {a - 2020;\,\,b - 2020;\,\,c - 2020} \right\}\).
\( \Leftrightarrow \left[ \begin{array}{l}{m^2} = 2\\{m^2} = - 2\\2 < {m^2} < 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \pm \sqrt 2 \\ - \sqrt 6 < m < \sqrt 2 \\\sqrt 2 < m < \sqrt 6 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - \sqrt 6 < m \le \sqrt 2 \\\sqrt 2 \le m < \sqrt 6 \end{array} \right.\).
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2;2} \right\}\).
Vậy có 2 giá trị nguyên của tham số \(m\) thỏa mãn yêu cầu bài toán.
Chọn B.







