Phương pháp giải:

Đồ thị hàm số \(y = {x^3} + 2020x + m\)  và trục hoành có điểm chung \( \Leftrightarrow \)  phương trình hoành độ giao điểm của hai đồ thị hàm số \({x^3} + 2020x + m = 0\) \( \Leftrightarrow {x^3} + 2020x =  - m\)  có nghiệm.

\( \Leftrightarrow \) Đường thẳng \(y =  - m\)  và đồ thị hàm số \(y = {x^3} + 2020x\)  có điểm chung.

Lập BBT rồi xác định số giá trị của \(m\)  thỏa mãn bài toán.

Lời giải chi tiết:

Đồ thị hàm số \(y = {x^3} + 2020x + m\)  và trục hoành có điểm chung \( \Leftrightarrow \)  phương trình hoành độ giao điểm của hai đồ thị hàm số \({x^3} + 2020x + m = 0\) \( \Leftrightarrow {x^3} + 2020x =  - m\)  có nghiệm.

\( \Leftrightarrow \) Đường thẳng \(y =  - m\)  và đồ thị hàm số \(y = {x^3} + 2020x\)  có điểm chung.

Xét hàm số \(y = {x^3} + 2020x\) ta có: \(y' = 3{x^2} + 2020 > 0\,\,\forall x\)

\( \Rightarrow \)  Hàm số \(y = {x^3} + 2020x\) đồng biến trên \(\mathbb{R}.\)

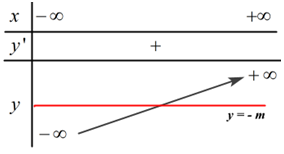
Ta có BBT:

\( \Rightarrow \)  Với mọi giá trị của \(m\)  thì đường thẳng \(y =  - m\) cắt đồ thị hàm số \(y = {x^3} + 2020x\)  tại 1 điểm.

Vậy có vô số giá trị của \(m\)  thỏa mãn bài toán.

Chọn A.