Phương pháp giải:

- Chứng minh \(d\left( {O;\left( P \right)} \right)\) đạt giá trị lớn nhất thì hình chiếu \(H\) của \(O\) lên \(\left( P \right)\) nằm trên \(AB\).

- Viết phương trình đường thẳng \(AB\).

- Tham số họa tọa độ điểm \(H\) thuộc \(AB\) theo tham số \(t\).

- Giải phương trình \(\overrightarrow {OH} .\overrightarrow {AB}  = 0\) tìm \(t\), từ đó suy ra VTPT của \(\left( P \right)\).

- Viết phương trình \(\left( P \right)\) đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) là:

\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

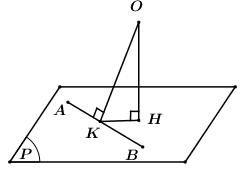
Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(O\) lên \(\left( P \right)\) và \(AB\).

Ta có \(OH \bot \left( P \right) \Rightarrow OH \bot HK \Rightarrow \Delta OHK\) vuông tại \(H\) \( \Rightarrow OH \le OK \Rightarrow d\left( {O;\left( P \right)} \right) \le OK\).

Do \(O,\,\,A,\,\,B\) cố định \( \Rightarrow OK\) không đổi.

\( \Rightarrow d\left( {O;\left( P \right)} \right)\) đạt giá trị lớn nhất bằng \(OK \Leftrightarrow H \equiv K\), khi đó \(H \in AB\).

Ta có \(A\left( { - 1;1;1} \right),B\left( {1;0;1} \right) \Rightarrow \overrightarrow {AB}  = \left( {2; - 1;0} \right)\), suy ra phương trình đường thẳng AB là \(\left\{ \begin{array}{l}x = 1 + 2t\\y =  - t\\z = 1\end{array} \right.\).

Gọi \(H\left( {1 + 2t;\,\, - t;\,\,1} \right) \in AB\) \( \Rightarrow \overrightarrow {OH} \left( {1 + 2t;\,\, - t;\,\,1} \right)\).

Mà \(OH \bot \left( P \right) \Rightarrow \) \(\overrightarrow {OH} .\overrightarrow {AB}  = 0\) \( \Leftrightarrow 2\left( {1 + 2t} \right) + t = 0 \Leftrightarrow t =  - \dfrac{2}{5}\)

\( \Rightarrow H\left( {\dfrac{1}{5};\dfrac{2}{5};1} \right)\)\( \Rightarrow \overrightarrow {OH} \left( {\dfrac{1}{5};\dfrac{2}{5};1} \right)\).

Vì \(OH \bot \left( P \right)\) nên \(\left( P \right)\) có 1 VTPT \(\overrightarrow {{n_P}}  = 5\overrightarrow {OH}  = \left( {1;2;5} \right)\).

Vậy phương trình mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến là \(\overrightarrow n \left( {1;2;5} \right)\) và đi qua \(A\left( { - 1;1;1} \right)\) là:

\(1\left( {x + 1} \right) + 2\left( {y - 1} \right) + 5\left( {z - 1} \right) = 0\) \( \Leftrightarrow x + 2y + 5z - 6 = 0\).

Chọn B.