Câu hỏi
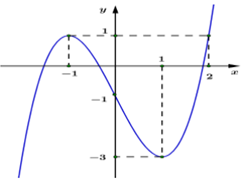
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên. Gọi \(g\left( x \right) = f\left( x \right) - \frac{1}{3}{x^3} + \frac{1}{2}{x^2} + x - 2019\). Biết \(g\left( { - 1} \right) + g\left( 1 \right) > g\left( 0 \right) + g\left( 2 \right)\), với \(x \in \left[ { - 1;2} \right]\) thì \(g\left( x \right)\) đạt giá trị nhỏ nhất bằng:
- A \(g\left( 2 \right)\)
- B \(g\left( 1 \right)\)
- C \(g\left( { - 1} \right)\)
- D \(g\left( 0 \right)\)
Phương pháp giải:
Tìm đạo hàm của hàm số.
Áp dụng tích phân để tìm gía trị nhỏ nhất của hàm số.
Lời giải chi tiết:
Ta có \(g\left( x \right) = f\left( x \right) - \frac{1}{3}{x^3} + \frac{1}{2}{x^2} + x - 2019\)
\( \Rightarrow g'\left( x \right) = f'\left( x \right) - {x^2} + x + 1\)
Đồ thị hàm số \(y = f'\left( x \right);y = {x^2} - x - 1\) cắt nhau tại 3 điểm có hoành độ là \( - 1;0;2\)
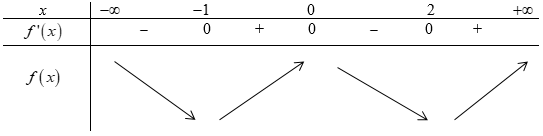
Bảng biến thiên:
Để tìm giá trị nhỏ nhất của \(g\left( x \right)\) thì ta đi so sánh \(g\left( { - 1} \right);g\left( 2 \right)\).
Ta có \(\int_{ - 1}^0 {g'\left( x \right)dx} < \int_2^0 {g'\left( x \right)dx} \Leftrightarrow g\left( 0 \right) - g\left( { - 1} \right) < g\left( 0 \right) - g\left( 2 \right) \Rightarrow g\left( { - 1} \right) > g\left( 2 \right)\)
Chọn A.