Câu hỏi
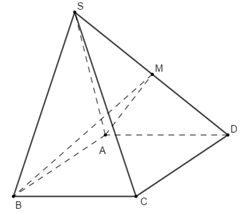
Cho khối chóp S.ABCD có thể tích bằng \(4{a^3}\), đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng \({a^2}\). Tính khoảng cách từ M tới mặt phẳng \(\left( {SAB} \right)\).
- A \(12a\)
- B \(6a\)
- C \(3a\)
- D \(4a\)
Phương pháp giải:
Sử dụng tỉ số thể tích để tính \({V_{SABM}}\).
Áp dụng công thức tính thể tích để suy ra \({d_{M;\left( {SAB} \right)}}\)
Lời giải chi tiết:
Vì M là trung điểm của SD nên \(\frac{{{V_{SABM}}}}{{{V_{SABD}}}} = \frac{{SM}}{{SD}} = \frac{1}{2}\)
Mà \(\frac{{{V_{SABD}}}}{{{V_{SABCD}}}} = \frac{1}{2} \Rightarrow {V_{SABD}} = \frac{1}{2}.4{a^3} = 2{a^3}\)
\( \Rightarrow {V_{SABM}} = {a^3} = \frac{1}{3}.d\left( {M;\left( {SAB} \right)} \right).{S_{SAB}} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \frac{{3{a^3}}}{{{a^2}}} = 3a\)
Chọn C.
Câu hỏi trước
