Câu hỏi
Hình nón có đường sinh \(l = 2a\) và hợp với đáy góc \(\alpha = {60^0}.\) Diện tích toàn phần của hình nón bằng:
- A \(4\pi {a^2}\)
- B \(3\pi {a^2}\)
- C \(2\pi {a^2}\)
- D \(\pi {a^2}\)
Phương pháp giải:
Công thức tính diện tích toán phần hình nón có bán kính đáy \(R,\;\)đường sinh \(l:\;\) \(\;{S_{tp}} = \pi Rl + \pi {R^2}.\)
Lời giải chi tiết:
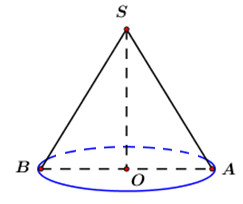
Đường sinh \(SA\) của hình nón hợp với đáy góc \(\alpha = {60^0}\) \( \Rightarrow \angle SAO = {60^0}\)
\( \Rightarrow OA = SA.\cos {60^0}\) \( = 2a.\dfrac{1}{2} = a.\)
\( \Rightarrow {S_{tp}} = \pi Rl + \pi {R^2}\) \( = \pi .a.2a + \pi {a^2} = 3\pi {a^2}.\)
Chọn B.
Câu hỏi trước
