Câu hỏi
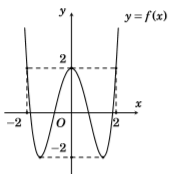
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Có baonhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ {0;20} \right]\) sao cho giá trịnhỏ nhất của hàm số \(g\left( x \right) = \left| {\left| {2f\left( x \right) + m + 4} \right| - f\left( x \right) - 3} \right|\) trên đoạn \(\left[ { - 2;2} \right]\) không bé hơn 1?
- A \(18\)
- B \(19\)
- C \(20\)
- D \(21\)
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy với \(x \in \left[ { - 2;2} \right]\) thì \(f\left( x \right) \in \left[ { - 2;2} \right]\) \( \Rightarrow 2f\left( x \right) \in \left[ { - 4;4} \right]\) \( \Leftrightarrow 2f\left( x \right) + 4 \in \left[ {0;8} \right]\).
Lại có \(m \in \left[ {0;20} \right]\,\,\left( {gt} \right)\) nên \(2f\left( x \right) + m + 4 > 0\,\,\forall x \in \left[ { - 2;2} \right],\,\,m \in \left[ {0;20} \right]\).
\(\begin{array}{l} \Rightarrow \left| {2f\left( x \right) + m + 4} \right| = 2f\left( x \right) + m + 4\\ \Rightarrow g\left( x \right) = \left| {\left| {2f\left( x \right) + m + 4} \right| - f\left( x \right) - 3} \right|\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left| {2f\left( x \right) + m + 4 - f\left( x \right) - 3} \right|\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left| {f\left( x \right) + m + 1} \right|\,\,\forall x \in \left[ { - 2;2} \right]\end{array}\)
Ta có: \(f\left( x \right) \in \left[ { - 2;2} \right] \Rightarrow f\left( x \right) + 1 \in \left[ { - 1;3} \right]\).
TH1: \(m = 0 \Rightarrow g\left( x \right) = \left| {f\left( x \right) + 1} \right| \in \left[ {0;3} \right]\), khi đó \(\mathop {\min }\limits_{\left[ { - 2;2} \right]} g\left( x \right) = 0\) (không thỏa mãn).
TH2: \(m \ne 0 \Leftrightarrow m \in \left[ {1;20} \right]\), khi đó \(f\left( x \right) + m + 1 \ge 0\,\,\forall x \in \left[ { - 2;2} \right]\).
\( \Rightarrow g\left( x \right) = \left| {f\left( x \right) + m + 1} \right| = f\left( x \right) + m + 1 \in \left[ { - 1 + m;3 + m} \right]\).
\( \Rightarrow \mathop {\min }\limits_{\left[ { - 2;2} \right]} g\left( x \right) = - 1 + m\) .
\( \Rightarrow - 1 + m \ge 1 \Leftrightarrow m \ge 2\), kết hợp điều kiện của \(m\) suy ra \(m \in \left[ {2;20} \right]\).
Vậy có 19 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Chọn B.







