Phương pháp giải:

Giả sử mặt phẳng qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông \(SAB\).

- Gọi \(M\) là trung điểm của \(AB\), trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\,\,\left( {H \in SM} \right)\), chứng minh \(OH \bot \left( {SAB} \right)\).

- Xác định góc giữa \(SO\) và \(\left( {SAB} \right)\) là góc giữa \(SO\) và hình chiếu của \(SO\) lên \(\left( {SAB} \right)\).

- Dựa vào diện tích tam giác \(SAB\), tính độ dài các cạnh của tam giác \(ABC\).

- Sử dụng tỉ số lượng giác của góc nhọn và định lí Pytago trong tam giác vuông tính \(SO,\,\,OA\).

- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(R\) là \(V = \dfrac{1}{3}\pi {R^2}h\).

Lời giải chi tiết:

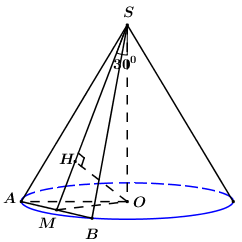
Giả sử mặt phẳng qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông \(SAB\).

Gọi \(M\) là trung điểm của \(AB\) \( \Rightarrow OM \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).

Trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\,\,\left( {H \in SM} \right)\) ta có: \(\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OH\).

\(\left\{ \begin{array}{l}OH \bot AB\\OH \bot SM\end{array} \right. \Rightarrow OH \bot \left( {SAB} \right)\) \( \Rightarrow SH\) là hình chiếu của \(SO\) lên \(\left( {SAB} \right)\).

\( \Rightarrow \angle \left( {SO;\left( {SAB} \right)} \right) = \angle \left( {SO;SH} \right) = \angle HSO = \angle MSO = {30^0}\).

Theo bài ra ta có \({S_{\Delta SAB}} = 4\) \( \Leftrightarrow \dfrac{1}{2}SA.SB = 4 \Leftrightarrow S{A^2} = 8 \Leftrightarrow SA = 2\sqrt 2 \).

Tam giác \(SAB\) vuông cân tại \(S\) \( \Rightarrow AB = SA\sqrt 2  = 2\sqrt 2 .\sqrt 2  = 4\) \( \Rightarrow SM = \dfrac{1}{2}AB = 2\).

Xét tam giác vuông \(SOM\)có: \(\left\{ \begin{array}{l}SO = SM.\cos {30^0} = 2.\dfrac{{\sqrt 3 }}{2} = \sqrt 3  = h\\OM = SM.\sin {30^0} = 2.\dfrac{1}{2} = 1\end{array} \right.\).

Áp dụng định lí Pytago trong tam giác vuông \(OAM\) có:

\(OA = \sqrt {O{M^2} + A{M^2}}  = \sqrt {{1^2} + {2^2}}  = \sqrt 5  = R\).

Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {\left( {\sqrt 5 } \right)^2}.\sqrt 3  = \dfrac{{5\sqrt 3 \pi }}{3}\).

Chọn D.