Phương pháp giải:

- Trong $\left( {ABCD} \right)$ kéo dài $AD$ cắt $BC$ tại $E$. Sử dụng định lí Ta-lét đảo chứng minh $MD\parallel BE$.

- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song và chứa đường thẳng kia.

- Đổi về tính khoảng cách từ $I$ đến $\left( {SBE} \right)$.

- Trong $\left( {SBE} \right)$ kẻ $IH \bot BE\,\,\left( {H \in BE} \right)$, trong $\left( {SIH} \right)$ kẻ $IK \bot SH\,\,\left( {K \in SH} \right)$, chứng minh $IK \bot \left( {SBE} \right)$.

- Xác định góc giữa $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

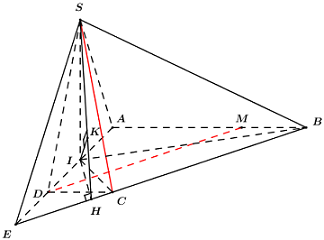
Trong $\left( {ABCD} \right)$ kéo dài $AD$ cắt $BC$ tại $E$, áp dụng định lí Ta-lét ta có: $\dfrac{{ED}}{{EA}} = \dfrac{{CD}}{{AB}} = \dfrac{a}{{3a}} = \dfrac{{BM}}{{BA}}$.

$\Rightarrow MD\parallel BE$ (định lí Ta-lét đảo) $\Rightarrow MD\parallel \left( {SBE} \right) \supset SC$ $\Rightarrow d\left( {MD;SC} \right) = d\left( {MD;\left( {SBE} \right)} \right) = d\left( {D;\left( {SBE} \right)} \right)$.

Ta có: $\left\{ \begin{array}{l}\left( {SBI} \right) \cap \left( {SCI} \right) = SI\\\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)$.

Lại có $DI \cap \left( {SBE} \right) = E$ $\Rightarrow \dfrac{{d\left( {D;\left( {SBE} \right)} \right)}}{{d\left( {I;\left( {SBE} \right)} \right)}} = \dfrac{{DE}}{{IE}}$.

Ta có: $\dfrac{{ED}}{{EA}} = \dfrac{{CD}}{{AB}} = \dfrac{1}{3} \Rightarrow \dfrac{{ED}}{{DA}} = \dfrac{1}{2}$ $\Rightarrow ED = \dfrac{1}{2}AD = \dfrac{a}{2}$, $IE = ED + DI = \dfrac{a}{2} + \dfrac{a}{2} = a$.

$\Rightarrow \dfrac{{DE}}{{IE}} = \dfrac{1}{2} \Rightarrow d\left( {D;\left( {SBE} \right)} \right) = \dfrac{1}{2}d\left( {I;\left( {SBE} \right)} \right)$.

Trong $\left( {SBE} \right)$ kẻ $IH \bot BE\,\,\left( {H \in BE} \right)$, trong $\left( {SIH} \right)$ kẻ $IK \bot SH\,\,\left( {K \in SH} \right)$ ta có:

$\begin{array}{l}\left\{ \begin{array}{l}BE \bot IH\\BE \bot SI\end{array} \right. \Rightarrow BE \bot \left( {SIH} \right) \Rightarrow BE \bot IK\\\left\{ \begin{array}{l}IK \bot BE\\IK \bot SH\end{array} \right. \Rightarrow IK \bot \left( {SBE} \right)\\ \Rightarrow d\left( {I;\left( {SBE} \right)} \right) = IK\end{array}$

Ta có: $BE \bot \left( {SIH} \right) \Rightarrow BE \bot SH$.

$\left\{ \begin{array}{l}\left( {SBE} \right) \cap \left( {ABCD} \right) = BE\\SH \subset \left( {SBE} \right),\,\,SH \bot BE\\IH \subset \left( {ABCD} \right),\,\,IH \bot BE\end{array} \right.$ $\Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {\left( {SBE} \right);\left( {ABCD} \right)} \right) = \angle \left( {SH;IH} \right) = \angle SHI = {60^0}$.

Ta có:

$\begin{array}{l}\left\{ \begin{array}{l}{S_{ABCD}} = \dfrac{{AD.\left( {AB + CD} \right)}}{2} = \dfrac{{a.\left( {3a + a} \right)}}{2} = 2{a^2}\\{S_{CDI}} = \dfrac{1}{2}CD.CI = \dfrac{1}{2}.a.\dfrac{a}{2} = \dfrac{{{a^2}}}{4}\\{S_{ABI}} = \dfrac{1}{2}AB.AI = \dfrac{1}{2}.3a.\dfrac{a}{2} = \dfrac{{3{a^2}}}{4}\end{array} \right.\\ \Rightarrow {S_{IBC}} = {S_{ABCD}} - {S_{CDI}} - {S_{ABI}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2{a^2} - \dfrac{{{a^2}}}{4} - \dfrac{{3{a^2}}}{4} = {a^2}\end{array}$

$BC = \sqrt {{{\left( {AB - CD} \right)}^2} + A{D^2}}  = \sqrt {4{a^2} + {a^2}}  = a\sqrt 5$.

Mặt khác ta lại có ${S_{IBC}} = \dfrac{1}{2}IH.BC$ $\Rightarrow IH = \dfrac{{2{S_{IBC}}}}{{BC}} = \dfrac{{2{a^2}}}{{a\sqrt 5 }} = \dfrac{{2a}}{{\sqrt 5 }}$.

Xét tam giác vuông $IHK$ có: $IK = IH.\sin {60^0} = \dfrac{{2a}}{{\sqrt 5 }}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt {15} }}{5}$.

Vậy $d\left( {MD;SC} \right) = \dfrac{1}{2}IK = \dfrac{{a\sqrt {15} }}{{10}}$.

Chọn B.