Phương pháp giải:

Công thức tính biên độ và pha ban đầu của dao động tổng hợp:

\(\left\{ \begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}.cos\Delta \varphi \\tan\varphi  = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}.\sin {\varphi _2}}}{{{A_1}\cos {\varphi _1} + {A_2}.cos{\varphi _2}}}\end{array} \right.\)

Sử dụng kiến thức toán học về giá trị nhỏ nhất/lớn nhất của hàm bậc 2.

Lời giải chi tiết:

Biên độ của dao động tổng hợp:

\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}.cos\Delta \varphi \\ \Leftrightarrow {A^2} = A_1^2 + {6^2} + 2.{A_1}.6.\cos \left[ {\dfrac{\pi }{6} - \left( { - \dfrac{\pi }{2}} \right)} \right]\\ \Leftrightarrow {A^2} = A_1^2 - 6{A_1} + 36\end{array}\)

Hàm A phụ thuộc vào A₁ có đồ thị là một parabol có bề lõm hướng lên.

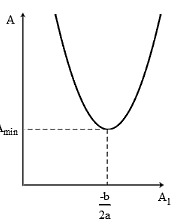
Tại đỉnh của parabol: \({A_1} =  - \dfrac{b}{{2a}} =  - \dfrac{{ - 6}}{{2.1}} = 3cm\) thì A nhận giá trị nhỏ nhất.

Pha ban đầu của dao động tổng hợp:

\(\begin{array}{l}tan\varphi  = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}.\sin {\varphi _2}}}{{{A_1}\cos {\varphi _1} + {A_2}.cos{\varphi _2}}} = \dfrac{{3.\sin \dfrac{\pi }{6} + 6.\sin \left( { - \dfrac{\pi }{2}} \right)}}{{3.cos\dfrac{\pi }{6} + 6.cos\left( { - \dfrac{\pi }{2}} \right)}} =  - \sqrt 3 \\ \Rightarrow \varphi  =  - \dfrac{\pi }{3}rad\end{array}\)

Chọn B.