Câu hỏi
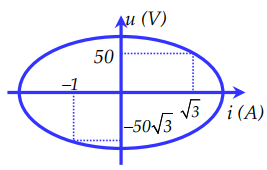
Cho đồ thị biểu diễn mối liên hệ giữa u và i trong mạch điện xoay chiều chỉ có L như hình vẽ. Xác định giá trị cảm kháng của cuộn cảm:
- A 100 Ω.
- B \(50{\sqrt 2 _{}}\Omega \)
- C 50Ω
- D 200 Ω
Phương pháp giải:
Đối với đoạn mạch chỉ chứa cuộn cảm:
\(\left\{ \begin{array}{l}
u = {U_0}.\cos \left( {\omega t + \varphi } \right)\\
i = {I_0}.\cos \left( {\omega t + \varphi - \frac{\pi }{2}} \right)
\end{array} \right.\)
Vì u và i vuông pha với nhau nên ta có \(\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\), đồ thị u phụ thuộc vào i là một elip.
Từ đồ thị ta xác định được hai vị trí tọa độ:
\(\left\{ \begin{array}{l}
\left( {{u_1};{i_1}} \right) = \left( {50;\sqrt 3 } \right)\\
\left( {{u_2};{i_2}} \right) = \left( { - 50\sqrt 3 ; - 1} \right)
\end{array} \right.\)
thay vào phương trình trên tìm được U0 và I0.
Và theo định luật Ôm ta có \({U_0} = {I_0}.{Z_L}\)
Lời giải chi tiết:
Đối với đoạn mạch chỉ chứa cuộn cảm:
\(\left\{ \begin{array}{l}
u = {U_0}.\cos \left( {\omega t + \varphi } \right)\\
i = {I_0}.\cos \left( {\omega t + \varphi - \frac{\pi }{2}} \right)
\end{array} \right.\)
Vì u và i vuông pha với nhau nên: \(\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1\)
→ Đồ thị u phụ thuộc vào i là một elip.
Từ đồ thị ta xác định được hai vị trí có tọa độ:
\(\left\{ \begin{array}{l}
\left( {{u_1};{i_1}} \right) = \left( {50;\sqrt 3 } \right)\\
\left( {{u_2};{i_2}} \right) = \left( { - 50\sqrt 3 ; - 1} \right)
\end{array} \right.\)
Thay vào (*) được:
\(\left\{ \begin{array}{l}
\frac{{{{50}^2}}}{{U_0^2}} + \frac{{{{\left( {\sqrt 3 } \right)}^2}}}{{I_0^2}} = 1\\
\frac{{{{\left( {50\sqrt 3 } \right)}^2}}}{{U_0^2}} + \frac{{{{\left( { - 1} \right)}^2}}}{{I_0^2}} = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{U_0} = 100V\\
{I_0} = 2A
\end{array} \right.\)
Áp dụng định luật Ôm:
\({I_0} = \frac{{{U_0}}}{{{Z_L}}} \Rightarrow {Z_L} = \frac{{{U_0}}}{{{I_0}}} = \frac{{100}}{2} = 50\Omega \)
Chọn C.







