Câu hỏi
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(C\), \(AB = 2a\) và góc tạo bởi hai mặt phẳng \(\left( {ABC'} \right)\) và \(\left( {ABC} \right)\) bằng \({60^0}\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(A'C'\) và \(BC\). Mặt phẳng \(\left( {AMN} \right)\) chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ bằng:
- A \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
- B \(\dfrac{{7\sqrt 6 {a^3}}}{{24}}\)
- C \(\dfrac{{\sqrt 6 {a^3}}}{6}\)
- D \(\dfrac{{7\sqrt 3 {a^3}}}{{24}}\)
Phương pháp giải:
- Xác định thiết diện của lăng trụ khi cắt bởi \(\left( {AMN} \right)\).
- Sử dụng định lí: Giao tuyến của ba mặt phẳng phân biệt hoặc đôi một song song, hoặc đồng quy.
- Sử dụng tỉ lệ thể tích Simpson.
- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Áp dụng công thức tính thể tích lăng trụ: \(V = Bh\) trong đó \(B,\,\,h\) lần lượt là chiều cao và diện tích đáy.
Lời giải chi tiết:
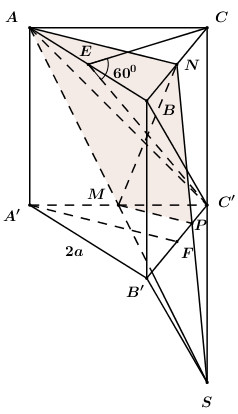
Giả sử \(\left( {AMN} \right) \cap \left( {A'B'C'} \right) = MP\) ta có:
\(\left\{ \begin{array}{l}\left( {AMN} \right) \cap \left( {ABC} \right) = AN\\\left( {AMN} \right) \cap \left( {A'B'C'} \right) = MP\\\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\end{array} \right. \Rightarrow AN\parallel MP\). Khi đó \(\left( {AMN} \right) \equiv \left( {AMPN} \right)\) và thiết diện của lăng trụ cắt bởi \(\left( {AMN} \right)\) là tứ giác \(AMPN\). Và mặt phẳng này chia khối lăng trụ thành hai phần: \(ANC.MPC'\) và \(ABN.A'B'PM\).
Ta lại có: \(\left\{ \begin{array}{l}\left( {AMPN} \right) \cap \left( {ACC'A'} \right) = AM\\\left( {AMPN} \right) \cap \left( {BCC'B'} \right) = PN\\\left( {ACC'A'} \right) \cap \left( {BCC'B'} \right) = CC'\end{array} \right.\) \( \Rightarrow AM,\,\,PN,\,\,CC'\) đồng quy tại \(S\).
Gọi \(F\) là trung điểm của \(B'C'\) ta có \(A'F\parallel AN\parallel MP\), do đó \(MP\) là đường trung bình của tam giác \(A'C'F\) \( \Rightarrow \dfrac{{MP}}{{A'F}} = \dfrac{1}{2} = \dfrac{{MP}}{{AN}}\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{MP}}{{AN}} = \dfrac{{SP}}{{SN}} = \dfrac{{SM}}{{SA}} = \dfrac{{SC'}}{{SC}} = \dfrac{1}{2}\).
Khi đó ta có: \(\dfrac{{{V_{S.MPC'}}}}{{{V_{S.ANC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SP}}{{SN}}.\dfrac{{SC'}}{{SC}} = \dfrac{1}{8}\) \( \Rightarrow {V_{S.MNC'}} = \dfrac{1}{8}{V_{S.ANC}} \Rightarrow {V_{ANC.MPC'}} = \dfrac{7}{8}{V_{S.ANC}}\).
Ta có: \({V_{S.ANC}} = \dfrac{1}{3}SC.{S_{ANC}} = \dfrac{1}{3}.2CC'.\dfrac{1}{2}{S_{\Delta ABC}} = \dfrac{1}{3}{V_{ABC.A'B'C'}}\).
\( \Rightarrow {V_{ANC.MPC'}} = \dfrac{7}{{24}}{V_{ABC.A'B'C'}}\), do đó \(ANC.MPC'\) là phần có thể tích nhỏ hơn.
Tam giác \(ABC\) vuông cân tại \(C\) có \(CE = \frac{1}{2}AB = a\), \(\angle CEC' = {60^0}\) \( \Rightarrow CC' = CE.\tan {60^0} = a\sqrt 3 \).
\( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}.a\sqrt 2 .a\sqrt 2 = {a^2}\).
Gọi \(E\) là trung điểm của \(AB\) ta có: \(CE \bot AB\) (do tam giác \(ABC\) vuông cân tại \(C\)).
\( \Rightarrow \left\{ \begin{array}{l}AB \bot CE\\AB \bot CC'\end{array} \right. \Rightarrow AB \bot \left( {CC'E} \right) \Rightarrow AB \bot C'E\).
\(\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {ABC'} \right) = AB\\CE \subset \left( {ABC} \right),\,\,CE \bot AB\\C'E \subset \left( {ABC'} \right),\,\,C'E \bot AB\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABC'} \right)} \right) = \angle \left( {CE;C'E} \right) = \angle CEC' = {60^0}\).
Xét tam giác vuông \(CC'E\) có \(CE = \dfrac{1}{2}AB = a\), \(\angle CEC' = {60^0}\) \( \Rightarrow CC' = CE.\tan {60^0} = a\sqrt 3 \).
\( \Rightarrow {V_{ABC.A'B'C'}} = CC'.{S_{\Delta ABC}} = a\sqrt 3 .{a^2} = {a^3}\sqrt 3 \).
Vậy \({V_{ANC.MPC'}} = \dfrac{7}{{24}}{V_{ABC.A'B'C'}} = \dfrac{{7{a^3}\sqrt 3 }}{{24}}\).
Chọn D.







