Câu hỏi
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(M\),\(N\), \(P\), \(Q\), \(R\), \(S\) là tâm các mặt của hình lập phương. Thể tích khối bát diện đều tạo bởi sáu đỉnh \(M\), \(N\), \(P\), \(Q\), \(R\), \(S\) bằng:
- A \(\dfrac{{{a^3}\sqrt 2 }}{{24}}\)
- B \(\dfrac{{{a^3}}}{6}\)
- C \(\dfrac{{{a^3}}}{{12}}\)
- D \(\dfrac{{{a^3}}}{4}\)
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp có chiều cao \(h\), diện tích đáy \(B\) là \(V = \dfrac{1}{3}Bh\).
Lời giải chi tiết:
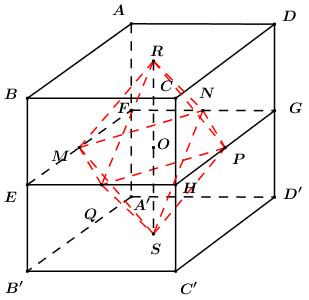
Gọi \(E,\,\,F,\,\,G,\,\,H\) lần lượt là trung điểm của \(BB',\,\,AA',\,\,DD',\,\,CC'\), khi đó ta có \(\left( {EFGH} \right) \equiv \left( {MNPQ} \right)\).
Gọi \(O\) là tâm hình lập phương, khi đo \(O\) là trung điểm của \(RS\) và \(RS \bot \left( {MNPQ} \right)\) tại \(O\).
Ta có:
\(\begin{array}{l}{V_{RSMNPQ}} = {V_{R.MNPQ}} + {V_{S.MNPQ}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}RO.{S_{MNPQ}} + \dfrac{1}{3}SO.{S_{MNPQ}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}RS.{S_{MNPQ}}\end{array}\)
Do \(EFGH\) là hình vuông cạnh \(a\) nên \(MN = NP = \dfrac{1}{2}EG = \dfrac{{a\sqrt 2 }}{2}\).
\( \Rightarrow {S_{MNPQ}} = MN.NP = \dfrac{{{a^2}}}{2}\), \(RS = a\).
Vậy \({V_{RS.MNPQ}} = \dfrac{1}{3}.a.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{6}\).
Chọn B.







