Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(f'\left( x \right)\) như hình vẽ. Số điểm cực trị của hàm số \(y = f\left( x \right)\) là:
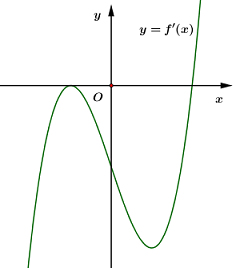
- A \(2\)
- B \(3\)
- C \(0\)
- D \(1\)
Phương pháp giải:
Số điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\) là số nghiệm bội lẻ của phương trình \(f'\left( x \right) = 0.\)
Hoặc số điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\) là số lần đổi dấu của \(f'\left( x \right).\)
Lời giải chi tiết:
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right)\) có 1 lần đổi dấu từ âm sang dương
\( \Rightarrow \) Hàm số \(y = f\left( x \right)\) có 1 điểm cực trị.
Chọn D.







