Câu hỏi
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 3,\,\,AD = 4,\,\,AA' = 5.\) Gọi \(O\) là tâm của đáy \(ABCD.\) Thể tích khối chóp \(O.A'B'C'\) bằng:
- A \(30\)
- B \(60\)
- C \(10\)
- D \(20\)
Phương pháp giải:
Công thức tính thể tích khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = \frac{1}{3}Sh.\)
Lời giải chi tiết:
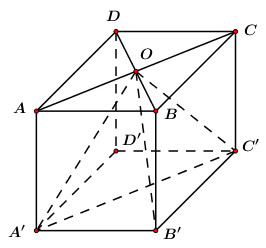
Ta có: \({V_{OA'B'C'}} = \frac{1}{3}d\left( {O;\,\,\left( {A'B'C'} \right)} \right).{S_{A'B'C'}}\)
\( = \frac{1}{3}AA'.\frac{1}{2}AB.AD = \frac{1}{6}.5.3.4 = 10.\)
Chọn C.
Câu hỏi trước
