Câu hỏi
Cho khối chóp S.ABCD có chiều cao bằng 9 và đáy là hình bình hành có diện tích bằng 10. Gọi M, N, P và Q lần lượt là trọng tâm các mặt bên SAB, SBC, SCD và SDA. Thể tích của khối đa diện lồi có đỉnh là các điểm M, N, P, Q, B và D bằng
- A \(9\)
- B \(\dfrac{{50}}{9}.\)
- C \(30\)
- D \(\dfrac{{25}}{3}.\)
Phương pháp giải:
- Xác định thiết diện \(A'B'C'D'\) của hình chóp cắt bởi mặt phẳng \(\left( {MNPQ} \right)\).
- Phân chia khối đa diện:
\(\begin{array}{l}{V_{MNPQBD}} = {V_{A'B'C'D'.ABCD}} - {V_{B.B'MN}} - {V_{D.D'PQ}} - {V_{A'MQ.ABD}} - {V_{C'NP.CBD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {V_{A'B'C'D'.ABCD}} - 2{V_{B.B'MN}} - 2{V_{A'MQ.ABD}}\end{array}\)
- Sử dụng công thức tính thể tích chóp cụt: \(V = \dfrac{1}{3}\left( {S + S' + \sqrt {S.S'} } \right).h\) với \(S,\,\,S'\) là diện tích hai đáy, \(h\) là chiều cao của khối chóp cụt.
Lời giải chi tiết:
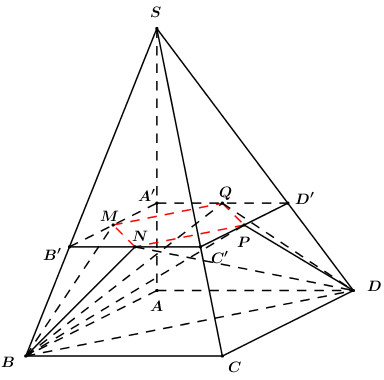
Thiết diện của hình chóp cắt bởi \(\left( {MNPQ} \right)\) là tứ giác \(A'B'C'D'\) như hình vẽ.
Khi đó ta có:
\(\begin{array}{l}{V_{MNPQBD}} = {V_{A'B'C'D'.ABCD}} - {V_{B.B'MN}} - {V_{D.D'PQ}} - {V_{A'MQ.ABD}} - {V_{C'NP.CBD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {V_{A'B'C'D'.ABCD}} - 2{V_{B.B'MN}} - 2{V_{A'MQ.ABD}}\end{array}\)
+) Ta có: Hình bình hành \(A'B'C'D'\) là \(ABCD\) đồng dạng theo tỉ số \(\dfrac{2}{3}\) nên \(\dfrac{{{S_{A'B'C'D'}}}}{{{S_{ABCD}}}} = {\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9}\) \( \Rightarrow {S_{A'B'C'D'}} = \dfrac{4}{9}{S_{ABCD}}\).
Lại có: \(d\left( {S;\left( {A'B'C'D'} \right)} \right) = \dfrac{2}{3}d\left( {S;\left( {ABCD} \right)} \right)\).
\(\begin{array}{l} \Rightarrow \dfrac{{{V_{S.A'B'C'D'}}}}{{{V_{S.ABCD}}}} = \dfrac{{\dfrac{1}{3}d\left( {S;\left( {A'B'C'D'} \right)} \right).{S_{A'B'C'D'}}}}{{\dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right).{S_{ABCD}}}} = \dfrac{2}{3}.\dfrac{4}{9} = \dfrac{8}{{27}}\\ \Rightarrow {V_{S.A'B'C'D'}} = \dfrac{8}{{27}}{V_{S.ABCD}}\\ \Rightarrow {V_{A'B'C'D'.ABCD}} = \left( {1 - \dfrac{8}{{27}}} \right){V_{S.ABCD}} = \dfrac{{19}}{{27}}{V_{S.ABCD}}\end{array}\)
+) Ta có \(BS \cap \left( {A'B'C'D'} \right) = B'\)
\(\begin{array}{l} \Rightarrow \dfrac{{d\left( {B;\left( {A'B'C'D'} \right)} \right)}}{{d\left( {S;\left( {A'B'C'D'} \right)} \right)}} = \dfrac{{BB'}}{{SB'}} = \dfrac{1}{2}\\ \Rightarrow d\left( {B;\left( {A'B'C'D'} \right)} \right) = \dfrac{1}{2}d\left( {S;\left( {A'B'C'D'} \right)} \right)\\ \Rightarrow d\left( {B;\left( {A'B'C'D'} \right)} \right) = \dfrac{1}{2}.\dfrac{2}{3}d\left( {S;\left( {ABCD} \right)} \right)\\ \Rightarrow d\left( {B;\left( {A'B'C'D'} \right)} \right) = \dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right)\end{array}\)
Lại có: \({S_{B'MN}} = \dfrac{1}{4}{S_{A'B'C'}} = \dfrac{1}{8}{S_{A'B'C'D'}} = \dfrac{1}{8}.\dfrac{4}{9}{S_{ABCD}} = \dfrac{1}{{18}}{S_{ABCD}}\)
\( \Rightarrow {V_{B.B'MN}} = \dfrac{1}{3}.\dfrac{1}{{18}} = \dfrac{1}{{54}}{V_{S.ABCD}}\).
+) \({S_{C'NP}} = {S_{B'MN}} = \dfrac{1}{{18}}{S_{ABCD}}\); \({S_{BCD}} = \dfrac{1}{2}{S_{ABCD}}\),
\(d\left( {\left( {A'B'C'D'} \right);\left( {ABCD} \right)} \right) = d\left( {B;\left( {A'B'C'D'} \right)} \right) = \dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right)\).
\(\begin{array}{l} \Rightarrow {V_{C'NP.CBD}} = \left( {\dfrac{1}{{18}}{S_{ABCD}} + \dfrac{1}{2}{S_{ABCD}} + \sqrt {\dfrac{1}{{18}}.\dfrac{1}{2}} {S_{ABCD}}} \right).\dfrac{1}{3}d\left( {S;\left( {ABCD} \right)} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{13}}{{54}}{S_{ABCD}}.d\left( {S;\left( {ABCD} \right)} \right) = \dfrac{{13}}{{54}}{V_{S.ABCD}}\end{array}\)
\( \Rightarrow \) \({V_{MNPQBD}} = \left( {\dfrac{{19}}{{27}} - 2.\dfrac{1}{{54}} - 2.\dfrac{{13}}{{54}}} \right){V_{S.ABCD}} = \dfrac{5}{{27}}{V_{S.ABCD}}\).
Mà \({V_{S.ABCD}} = \dfrac{1}{3}.9.10 = 30\).
Vậy \({V_{MNPQBD}} = \dfrac{5}{{27}}.30 = \dfrac{{50}}{9}\).
Chọn B.







