Phương pháp giải:

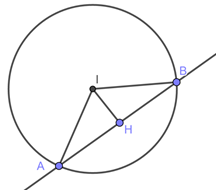
Bước 1: Gọi \(H\) là trung điểm dây \(AB \Rightarrow AH = HB = \frac{{AB}}{2}\) và \(IH \bot AB \Rightarrow IH = d\left( {I;d} \right)\)

Bước 2: Tính \({R^2} = A{I^2} = A{H^2} + I{H^2}\)(Áp dụng định lý Pithago trong tam giác vuông \(IAH\))

Bước 3: Lập phương trình đường tròn đi qua tâm \(I\) đã cho và bán kính \(R\) vừa tìm

Lời giải chi tiết:

Gọi \(H\) là trung điểm dây \(AB \Rightarrow AH = HB = \frac{{AB}}{2} = \frac{6}{2} = 3\) và \(IH \bot AB\)

\( \Rightarrow IH = d\left( {I;d} \right) = \frac{{\left| {3.\left( { - 1} \right) - 2 - 15} \right|}}{{\sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} = 2\sqrt {10} \)

Xét tam giác vuông \(IAH\)có: \(A{I^2} = I{H^2} + A{H^2} = {\left( {2\sqrt {10} } \right)^2} + {3^2} = 49\)

\( \Rightarrow {R^2} = 49\)

Phương trình đường tròn: \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 49\)\( \Leftrightarrow {x^2} + {y^2} + 2x - 4y - 44 = 0\)

Chọn A.